Difference between revisions of "Electric machines"
From ONELAB
(→References) |
(→Additional information) |
||
| Line 3: | Line 3: | ||
== Additional information == | == Additional information == | ||
| − | The | + | To run the models, open '''main.pro''' with Gmsh. The models include: |
* '''pmsm.pro''' and '''pmsm_cbmag.pro''': an eight-pole permanent magnet synchronous machine from GRUCAD, Universidade Federal de Santa Catarina, Brazil (the geometry of '''pmsm''' is a simplified version of '''pmsm_cbmag''')<ref name=Fer2002 /><ref name=Gys2002_pmsm /><ref name=Gys2003_hbfe /> | * '''pmsm.pro''' and '''pmsm_cbmag.pro''': an eight-pole permanent magnet synchronous machine from GRUCAD, Universidade Federal de Santa Catarina, Brazil (the geometry of '''pmsm''' is a simplified version of '''pmsm_cbmag''')<ref name=Fer2002 /><ref name=Gys2002_pmsm /><ref name=Gys2003_hbfe /> | ||
* '''lomonova.pro''': an eight-pole permanent magnet machine <ref name=Lom2011_pmsm /> | * '''lomonova.pro''': an eight-pole permanent magnet machine <ref name=Lom2011_pmsm /> | ||
| Line 12: | Line 12: | ||
* '''srm.pro''': a switch reluctance machine <ref name=Gys2011_cmag /><ref name=Gys2012_cefc /> | * '''srm.pro''': a switch reluctance machine <ref name=Gys2011_cmag /><ref name=Gys2012_cefc /> | ||
| − | All the | + | All the models are solved using a 2D vector potential formulation, coupled with circuit equations if necessary. Motion is solved with the moving band technique, except for '''t30.pro''' which can also be solved using a velocity term. |
== References == | == References == | ||
Revision as of 14:23, 2 September 2014
|
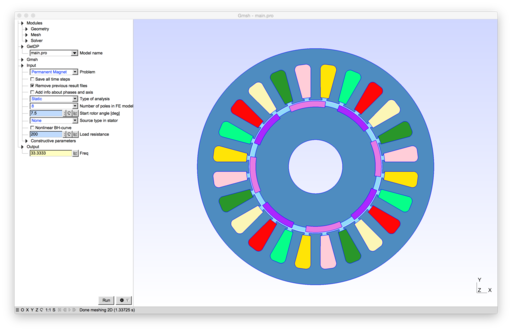
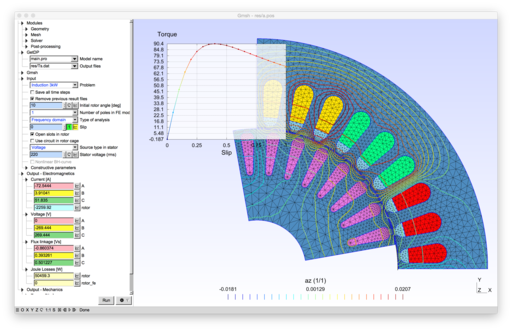
2D models of electric machines: permanent magnet and wound field synchronous machines, induction machines, switched reluctance machine.
|
|
|---|
|
Download model archive (machines.zip) |
Additional information
To run the models, open main.pro with Gmsh. The models include:
- pmsm.pro and pmsm_cbmag.pro: an eight-pole permanent magnet synchronous machine from GRUCAD, Universidade Federal de Santa Catarina, Brazil (the geometry of pmsm is a simplified version of pmsm_cbmag)[1][2][3]
- lomonova.pro: an eight-pole permanent magnet machine [4]
- wfsm_4p.pro: a four-pole wound field synchronous machine [5]
- t30.pro: an simple induction motor with solid rotor [6][7]
- im_3kw.pro: a four-pole induction machine [8][9][10]
- im.pro: a four-pole deep-bar induction machine [11]
- srm.pro: a switch reluctance machine [12][13]
All the models are solved using a 2D vector potential formulation, coupled with circuit equations if necessary. Motion is solved with the moving band technique, except for t30.pro which can also be solved using a velocity term.
References
- ↑ M. V. Ferreira da Luz, P. Dular, N. Sadowski, C. Geuzaine, and J. P. A. Bastos, Analysis of a permanent magnet generator with dual formulations using periodicity conditions and moving band, IEEE Trans. Mag., 38(2):961-964, 2002.
- ↑ J. Gyselinck, N. Sadowski, P. Dular, M. V. Ferreira da Luz, J. P. A. Bastos, and W. Legros, Harmonic balance finite element modelling of a permanent-magnet synchronous machine, Proceedings of the V Brazilian Conference on Electromagnetics (CBMag2002), 4-6 November 2002, Gramado, Brazil, 4 p.
- ↑ J. Gyselinck, P. Dular, L. Vandevelde and J. Melkebeek, A.M. Oliveira and P. Kuo-Peng, Two-dimensional harmonic balance finite element modelling of electrical machines taking motion into account, COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 22(4):1021-1036, 2003.
- ↑ E. A. Lomonova, E. Kazmin, Y. Tang, J. J. H. Paulides, In-wheel PM motor: Compromise between high power density and extended speed capability, COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engineering, 30(1):98-116, 2011.
- ↑ J. Gyselinck, L. Vandevelde, J. Melkebeek, W. Legros, Steady-state finite element analysis of a salient-pole synchronous machine in the frequency domain, Proceedings the 7th International Conference on Modeling and Simulation of Electric Machines, Converters and Systems (ELECTRIMACS2002), August 18-21, Montréal, Canada, 6 p.
- ↑ International TEAM Workshop Problem 30a - Induction Motor Analyses, Kent Davey
- ↑ TEAM Workshop Problem 30a – Three-phase induction motor problem, Infolytica gallery
- ↑ J. Gyselinck, Twee dimensionale dynamische eindige-elementenmodellering van statische en roterende elektromagnetische energieomzetters, Ph.D. Thesis, Universiteit Gent, 2000.
- ↑ J. Gyselinck, L. Vandevelde, J. Melkebeek, Multi-slice modeling of electrical machines with skewed slots - The skew discretization error, IEEE Trans. Magn., 37(5):3233–3237, 2002.
- ↑ J. Gyselinck, L. Vandevelde, P. Dular, C. Geuzaine, W. Legros, A general method for the frequency domain FE modelling of rotating electromagnetic devices, IEEE Trans. Magn., 39(3):1147-1150, 2003.
- ↑ S. Guérard, J. Gyselinck, and J. Lecomte-Beckers,Finite element modelling of an asynchronous motor with one broken rotor bar, comparison with the data recorded on a prototype and material aspects, Bulletin Scientifique de l'AIM, 1:13-22, 2005. Prix Melchior Salier 2004 du meilleur travail de fin d'études section électromécanique-énergétique.
- ↑ J. Gyselinck, C. Geuzaine, R. V. Sabariego, Considering laminated cores and eddy currents in 2D and 3D finite element simulation of electrical machines, In Proceedings of the 18th Conference on the Computation of Electromagnetic Fields (COMPUMAG2011), Sydney, Australia, July 12–15, 2011.
- ↑ J. Gyselinck, C. Geuzaine, R. V. Sabariego, Homogenisation of windings and laminations in time-domain finite-element modeling of electrical machines, In Proceedings of the 15th Biennial IEEE Conference on Electromagnetic Field Computation (CEFC2012), Oita, Japan, November 11– 14, 2012.
|
Models developed by R. Sabariego, J. Gyselinck and C. Geuzaine. This work was funded in part by the Walloon Region (WBGreen No 1217703 FEDO, WIST3 No 1017086 ONELAB) and by the Belgian Science Policy (IAP P7/02). Copyright (c) 2012-2015 ULg-ULB.
|
<references \>

