Difference between revisions of "Tutorial/Coupled problems"

From ONELAB
Jump to: navigation, search
(→‎The considered problem)
m (Geuzaine moved page Coupled problems to Tutorial/Coupled problems)
 
(77 intermediate revisions by 4 users not shown)
Line 1: Line 1:
−
== The considered problem ==
+
== Introduction ==
  
−
Here is explained how to use the solution of a first problem as a data for a second problem. Two kind of problem are studied here, depending if the solution of the first problem directly appears in the weak formulation (for example, as a source or a Neumann boundary), or if it is used a constraint (Dirichlet boundary condition).  
+
Here is explained how to use the solution of a first problem as a data in a second problem. Two kind of problem are studied here. In the "first" one, the solution of the first problem directly appears in the weak formulation of the second problem (for example, as a source or a Neumann boundary) whereas in the second kind of problem, the solution is used as a constraint (Dirichlet boundary condition), so it should appears in the function space. Note that a Lagrange multiplier could be used to force the Dirichlet constraint in the weak formulation.
  
−
== First coupled problem : solution appearing the weak formulation ==
+
== First kind of coupled problem : solution appearing in the weak formulation ==
  
−
Let us begin by the first example with the very simple following example. The computation domain is the unit square $\Omega = [0,1]\times[0,1]$ with boundary $\Gamma$ and unit outwardly directed normal $\mathbf{n}$.  
+
=== Mathematics ===
−
 
+
Let the computation domain be the unit square $\Omega = [0,1]\times[0,1]$ with boundary $\Gamma$ and unit outwardly directed normal $\mathbf{n}$. Consider the two coupled following problems : firstly, find $u$, solution of
−
The first coupled problem read as follows :
 
 
\begin{equation}
 
\begin{equation}
 
\begin{cases}\label{eq:problemU}
 
\begin{cases}\label{eq:problemU}
−
\Delta u = 0 & \text{in } \Omega,\\
+
-\Delta u + u = C & \text{in } \Omega,\\
−
u = C & \text{on }\Gamma,
+
\displaystyle{\frac{\partial u}{\partial \mathbf{n}} = 0} & \text{on }\Gamma,
 
\end{cases}
 
\end{cases}
 
\end{equation}
 
\end{equation}
Line 21: Line 20:
 
\end{cases}
 
\end{cases}
 
\end{equation}
 
\end{equation}
−
where $u$ is the solution of problem \ref{eq:problemU}. Obviously, solution $u$ is constant inside $\Omega$ and is equal to $C$ and there is no "real" need in solving problem \ref{eq:problemU}. The weak formulation of problems \ref{eq:problemU} and \ref{eq:problemV} read as :
+
where $u$ is the solution of problem \ref{eq:problemU}. Obviously, the function $u$ is the constant function equal to $C$ and thus, there is no "real" need in solving numerically problem \ref{eq:problemU}. However, please keep in mind that this is just an example. In order to solve numerically these problem using a finite element method, on has to write the weak formulations of problems \ref{eq:problemU} and \ref{eq:problemV}, which read as:
−
 
 
 
\begin{equation}\label{eq:WeakFormulationU}
 
\begin{equation}\label{eq:WeakFormulationU}
 
\left\{\begin{array}{l}
 
\left\{\begin{array}{l}
−
\text{Find } u\in H^1(\Omega) \text{ such that, $u|_{\Gamma} = C$ and}\\
+
\text{Find } u\in H^1(\Omega) \text{ such that}\\
−
\displaystyle{\forall u'\in H^1_0(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla u' \;{\rm d}\Omega = 0},
+
\displaystyle{\forall u'\in H^1(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla u' \;{\rm d}\Omega + \int_{\Omega} u\cdot u' \;{\rm d}\Omega - \int_{\Omega} Cu'\;{\rm d}\Omega = 0},
 
\end{array}\right.
 
\end{array}\right.
 
\end{equation}
 
\end{equation}
−
 
+
and
 
\begin{equation}\label{eq:WeakFormulationV}
 
\begin{equation}\label{eq:WeakFormulationV}
 
\left\{\begin{array}{l}
 
\left\{\begin{array}{l}
Line 36: Line 34:
 
\end{array}\right.
 
\end{array}\right.
 
\end{equation}
 
\end{equation}
−
where $H^1(\Omega)$ is the classical Sobolev space, $H^1_0(\Omega)$ is the space of $H^1(\Omega)$ functions which vanish at the boundary $\Gamma$.
+
where $H^1(\Omega)$ is the classical Sobolev space.
 +
 
 +
=== Computation in GetDP ===
 +
 
 +
In GetDP, this kind of problem is very easy to solve. Indeed, the user has to introduce two function space (one per solution), and ask GetDP to solve each problem in the right order. There is no trap ! Below are the GMSH and GetDP files. Compared to the other academic examples, the only new things are in the .pro file.
 +
 
 +
=== Files ===
 +
 
 +
There are two files :
 +
; FirstCoupledProblem.geo that contains the geometry and is used to mesh the domain
 +
; FirstCoupledProblem.pro that contains the weak formulations, function spaces, etc.
 +
 
 +
To solve the problem, type in a terminal (in the right directory) :
 +
: gmsh FirstPb.geo -2
 +
and then solve the problem with getdp :
 +
: getdp FirstPb.pro -solve -pos
 +
or directly
 +
: getdp FirstPb.pro -solve CoupledProblem -pos Map_u_and_v
 +
 
 +
{{GetDPTutorial|CoupledProblems/First/FirstPb.geo|height=22em}}
 +
{{GetDPTutorial|CoupledProblems/First/FirstPb.pro|height=22em}}
 +
 
 +
=== Result ===
 +
 
 +
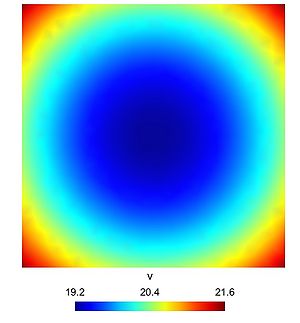
[[File:FirstCoupledPbv.jpg|300px|frameless|alt=Solution v.|v.]]
 +
 
 +
== Second kind of coupled problem : solution used as a Dirichlet boundary condition ==
 +
 
 +
=== Mathematics ===
 +
 
 +
In this section, the first problem (\ref{eq:problemU}) does not change but the second problem is now to find $v$, such that
 +
\begin{equation}
 +
\begin{cases}\label{eq:problemV2}
 +
-\Delta v + v = 0 & \text{in } \Omega,\\
 +
\displaystyle{v = u} & \text{on }\Gamma,
 +
\end{cases}
 +
\end{equation}
 +
where $u$ is the solution of (\ref{eq:problemU}). The function $u$ is now involved as a Dirichlet boundary condition and thus, will appear in the function space of $v$ (again, except if one uses a Lagrange multiplier, which is not the case here). To obtain the weak formulation of problem (\ref{eq:problemV2}), we introduce the following function space \ref{eq:WeakFormulationU}
 +
$$
 +
H^1_u(\Omega) = \left\{w\in H^1(\Omega) \text{ such that $w|_{\Gamma} = u|_{\Gamma}$, where $u$ is the solution of problem (1)} \right\}.
 +
$$
 +
Thus, we have
 +
\begin{equation}\label{eq:WeakFormulationV2}
 +
\left\{\begin{array}{l}
 +
\text{Find } v\in H^1_u(\Omega) \text{ such that, }\\
 +
\displaystyle{\forall v'\in H^1_0(\Omega), \qquad \int_{\Omega} \nabla v\cdot\nabla v' \;{\rm d}\Omega + \int_{\Omega}vv' \;{\rm d}\Omega = 0},
 +
\end{array}\right.
 +
\end{equation}
 +
 
 +
=== GetDP ===
 +
 
 +
In GetDP, a Dirichlet boundary condition is generally imposed through the "Constraint" term, it can be imposed with the help of a Lagrange multiplier.
 +
In the second case, the Dirichlet boundary condition is no more "imposed" in the function space but appears in the weak formulation (as a Neumann boundary condition). Thus, the previous case can be used. Here is only considered the first case using the GetDP function "AssignFromResolution". A Resolution dedicated to $u$ must then be created, in this example it will be named ''AuxiliaryResolution''. In GetDP, the procedure can be summarized as follows:
 +
* Create a constraint with :
 +
:: Type AssignFromResolution ; Resolution AuxiliaryResolution;
 +
* Construct only ONE function space that will contain $u$ and at the end $v$ ($u$ will be erased !)
 +
* Create two Resolution, one for $v$ and one for $u$ :
 +
** for $v$ : Generate, Solve, Save
 +
** for $u$ (AuxiliaryResolution) : Generate, Solve, TransfertSolution (do not Save !)
 +
 
 +
With this, GetDP will ... :
 +
 
 +
* Try to solve problem with $v$
 +
* Need the Dirichlet constraint (that is $u$)
 +
* Solve problem with $u$
 +
* Solve problem with $v$
 +
 
 +
Sometimes it is usefull to save both $u$ and $v$ at the end of the calculation. This can be done by adding an auxiliary problem that "copy" $u$ (see the last paragraph).
 +
 
 +
=== Files ===
 +
 
 +
There are two files :
 +
; Secondpb.geo : exactly the same as FirstPb.geo
 +
; Secondpb.pro : quite the same as FirstPb.pro
 +
 
 +
To solve the problem, type in a terminal (in the right directory) :
 +
: gmsh SecondPb.geo -2
 +
and then solve the problem with getdp :
 +
: getdp SecondPb.pro -solve -pos
 +
and chose the first resolution (MainResolution) or directly
 +
: getdp SecondPb.pro -solve MainResolution -pos Map_v
 +
 
 +
{{GetDPTutorial|CoupledProblems/Second/SecondPb.geo|height=22em}}
 +
{{GetDPTutorial|CoupledProblems/Second/SecondPb.pro|height=22em}}
 +
 
 +
=== Result ===
 +
 
 +
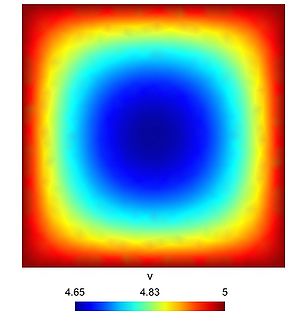
[[File:SecondCoupledPbv.jpg|300px|frameless|alt=Solution v.|v.]]
 +
 
 +
== Second kind of coupled problem with a save of solution $u$ ==
 +
 
 +
Sometimes, it can be usefull to save both $u$ and $v$. To achieved this, one can introduce an auxiliary variable $u_{aux}$ that will be a copy of $u$. Here, we proposed to add :
 +
; A new FunctionSpace to store $u$
 +
; A new weak formulation to copy $u$ into an auxiliary variable $u_{aux}$
 +
 
 +
The modified .pro file (SecondPbWithSave.pro) can be found below. The .geo file being exactly the same as the previous ones.
 +
 
 +
{{GetDPTutorial|CoupledProblems/SecondWithSave/SecondPbWithSave.geo|height=5em}}
 +
{{GetDPTutorial|CoupledProblems/SecondWithSave/SecondPbWithSave.pro|height=22em}}
 +
 
 +
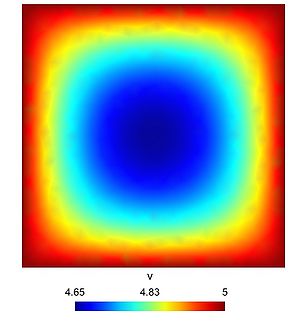
[[File:SecondCoupledPb2v.jpg|300px|frameless|alt=Solution v.|v.]]
 +
 
 +
== All files ==
 +
 
 +
A zipfile containing all files (.geo, .pro, .mesh and .pos) can be [http://onelab.info/files/getdp/CoupledProblems/CoupledProblems.zip downloaded here].

Latest revision as of 21:14, 19 April 2015

Introduction

Here is explained how to use the solution of a first problem as a data in a second problem. Two kind of problem are studied here. In the "first" one, the solution of the first problem directly appears in the weak formulation of the second problem (for example, as a source or a Neumann boundary) whereas in the second kind of problem, the solution is used as a constraint (Dirichlet boundary condition), so it should appears in the function space. Note that a Lagrange multiplier could be used to force the Dirichlet constraint in the weak formulation.

First kind of coupled problem : solution appearing in the weak formulation

Mathematics

Let the computation domain be the unit square $\Omega = [0,1]\times[0,1]$ with boundary $\Gamma$ and unit outwardly directed normal $\mathbf{n}$. Consider the two coupled following problems : firstly, find $u$, solution of \begin{equation} \begin{cases}\label{eq:problemU} -\Delta u + u = C & \text{in } \Omega,\\ \displaystyle{\frac{\partial u}{\partial \mathbf{n}} = 0} & \text{on }\Gamma, \end{cases} \end{equation} where $C$ is a constant. Then, find the solution $v$ of the second problem \begin{equation} \begin{cases}\label{eq:problemV} -\Delta v + v = 0 & \text{in } \Omega,\\ \displaystyle{\frac{\partial v}{\partial \mathbf{n}} = u} & \text{on }\Gamma, \end{cases} \end{equation} where $u$ is the solution of problem \ref{eq:problemU}. Obviously, the function $u$ is the constant function equal to $C$ and thus, there is no "real" need in solving numerically problem \ref{eq:problemU}. However, please keep in mind that this is just an example. In order to solve numerically these problem using a finite element method, on has to write the weak formulations of problems \ref{eq:problemU} and \ref{eq:problemV}, which read as: \begin{equation}\label{eq:WeakFormulationU} \left\{\begin{array}{l} \text{Find } u\in H^1(\Omega) \text{ such that}\\ \displaystyle{\forall u'\in H^1(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla u' \;{\rm d}\Omega + \int_{\Omega} u\cdot u' \;{\rm d}\Omega - \int_{\Omega} Cu'\;{\rm d}\Omega = 0}, \end{array}\right. \end{equation} and \begin{equation}\label{eq:WeakFormulationV} \left\{\begin{array}{l} \text{Find } v\in H^1(\Omega) \text{ such that, }\\ \displaystyle{\forall v'\in H^1(\Omega), \qquad \int_{\Omega} \nabla v\cdot\nabla v' \;{\rm d}\Omega + \int_{\Omega}vv' \;{\rm d}\Omega - \int_{\Gamma}uv'\;{\rm d}\Gamma = 0}, \end{array}\right. \end{equation} where $H^1(\Omega)$ is the classical Sobolev space.

Computation in GetDP

In GetDP, this kind of problem is very easy to solve. Indeed, the user has to introduce two function space (one per solution), and ask GetDP to solve each problem in the right order. There is no trap ! Below are the GMSH and GetDP files. Compared to the other academic examples, the only new things are in the .pro file.

Files

There are two files :

FirstCoupledProblem.geo that contains the geometry and is used to mesh the domain
FirstCoupledProblem.pro that contains the weak formulations, function spaces, etc.

To solve the problem, type in a terminal (in the right directory) :

gmsh FirstPb.geo -2

and then solve the problem with getdp :

getdp FirstPb.pro -solve -pos

or directly

getdp FirstPb.pro -solve CoupledProblem -pos Map_u_and_v
//Caracteristic length of the finite elements (reffinement is also possible after the mesh is built):
lc = 0.05;

// The parameters of the border of the domain :
x_max = 1;
x_min = 0;
y_max= 1;
y_min = 0;

//Creation of the 4 angle points of the domain Omega (=square)
p1 = newp; Point(p1) = {x_min,y_min,0,lc};
p2 = newp; Point(p2) = {x_min,y_max,0,lc};
p3 = newp; Point(p3) = {x_max,y_max,0,lc};
p4 = newp; Point(p4) = {x_max,y_min,0,lc};

//The four edges of the square
L1 = newreg; Line(L1) = {p1,p2};
L2 = newreg; Line(L2) = {p2,p3};
L3 = newreg; Line(L3) = {p3,p4};
L4 = newreg; Line(L4) = {p4,p1};

// Line Loop (= boundary of the square)
Bound = newreg; Line Loop(Bound) = {L1,L2,L3,L4};

//Surface of the square
SurfaceOmega = newreg; Plane Surface(SurfaceOmega) = {Bound};

// To conclude, we define the physical entities, that is "what GetDP could see/use".
// 1 is associtated to Omega
// 2 to Gamma
Physical Surface(1) = {SurfaceOmega};
Physical Line(2) = {L1,L2,L3,L4};
// Do not forget to let a blank line at the end, this could make GMSH crash...

Direct link to file `CoupledProblems/First/FirstPb.geo'

// Group
//======
Group{
Omega = Region[{1}];
Gama = Region[{2}];
}

// Function
//=========
Function{
C = 5; //constant C in the problem solved by u
}

//Jacobian
//========
Jacobian {
  { Name JVol ;
    Case {
      { Region All ; Jacobian Vol ; }
    }
  }
  { Name JSur ;
    Case {
      { Region All ; Jacobian Sur ; }
    }
  }
  { Name JLin ;
    Case {
      { Region All ; Jacobian Lin ; }
    }
  }
}

//Integration (parameters)
//=======================
Integration {
  { Name I1 ;
    Case {
      { Type Gauss ;
        Case {
          { GeoElement Point ; NumberOfPoints  1 ; }
          { GeoElement Line ; NumberOfPoints  4 ; }
          { GeoElement Triangle ; NumberOfPoints  6 ; }
          { GeoElement Quadrangle ; NumberOfPoints 7 ; }
          { GeoElement Tetrahedron ; NumberOfPoints 15 ; }
          { GeoElement Hexahedron ; NumberOfPoints 34 ; }
        }
      }
    }
  }
}

//FunctionSpace
//=============
FunctionSpace{
//Space for u
	{ Name Hgrad_u; Type Form0;
    BasisFunction{
      {Name wn; NameOfCoef vn; Function BF_Node;
    Support Region[{Omega, Gama}]; Entity NodesOf[All];}
    }
    }
//Space for v
	{ Name Hgrad_v; Type Form0;
    BasisFunction{
      {Name wn; NameOfCoef vn; Function BF_Node;
    Support Region[{Omega, Gama}]; Entity NodesOf[All];}
    }
  }
}
/*
The two FunctionSpaces are exactly the same. However, keep in mind that
a FunctionSpace can contain only one solution ! That is why we need two FunctionSpaces.
*/


//(Weak) Formulations
//==================

Formulation{
// Problem solved by u :
// Delta u + u = C (Omega)
// dn u = 0 (Gamma)
  {Name ProblemU; Type FemEquation;
    Quantity{
      {Name u; Type Local; NameOfSpace Hgrad_u;}
    }
    Equation{
      Galerkin{ [Dof{Grad u}, {Grad u}];
        In Omega; Jacobian JVol; Integration I1;}
      Galerkin{ [Dof{u}, {u}];
        In Omega; Jacobian JVol; Integration I1;}
      Galerkin{ [-C, {u}];
        In Omega; Jacobian JVol; Integration I1;}
    }
  }

// Coupled problem : "first kind" : 
// Neumann condition on Gamma 
// Delta v + v =0 Omega
// dn v = u on Gamma
  {Name ProblemV; Type FemEquation;
    Quantity{
    // v is the unknown
      {Name v; Type Local; NameOfSpace Hgrad_v;}
	// u is called but will NOT be used as an unknown (NO "Dof")
      {Name u; Type Local; NameOfSpace Hgrad_u;}
    }
    Equation{
      Galerkin{ [Dof{Grad v}, {Grad v}];
        In Omega; Jacobian JVol; Integration I1;}

      Galerkin{ [Dof{v}, {v}];
        In Omega; Jacobian JVol; Integration I1;}
		//Neumann condition on Gama (no "Dof" !)
      Galerkin{ [-{u}, {v}];
        In Gama; Jacobian JSur; Integration I1;}
    }
  }
  
  
}

// Resolution
//===========

Resolution{
// First coupled problem available
  {Name CoupledProblem;
    System{
      {Name PbU; NameOfFormulation ProblemU;}
      {Name PbV; NameOfFormulation ProblemV;}
    }
    Operation{
      Generate[PbU]; Solve[PbU]; SaveSolution[PbU];
      Generate[PbV]; Solve[PbV]; SaveSolution[PbV];
    }
/*Short explanations : GetDP will :
1) generate and solve the problem associated to "u" then save "u" in the space H1_C
2) generate and solve the problem associated to "v" and save "v" in the space H1
*/
  }
  
}


//Post Processing
//===============

PostProcessing{
  {Name CoupledProblem; NameOfFormulation ProblemV;
  //The associated formulation is "ProblemV" because it involves both "u" and "v"
  //(ProblemU only call "u", not "v")
    Quantity{
      {Name u; Value {Local{[{u}];In Omega; Jacobian JVol;}}}
      {Name v; Value {Local{[{v}];In Omega; Jacobian JVol;}}}
    }
  }
}

//Post Operation
//==============

PostOperation{
  {Name Map_u_and_v; NameOfPostProcessing CoupledProblem;
    Operation{
      Print[u, OnElementsOf Omega, File "sol_u.pos"];
      Print[v, OnElementsOf Omega, File "sol_v.pos"];
    }
  }
}

Direct link to file `CoupledProblems/First/FirstPb.pro'

Result

Solution v.

Second kind of coupled problem : solution used as a Dirichlet boundary condition

Mathematics

In this section, the first problem (\ref{eq:problemU}) does not change but the second problem is now to find $v$, such that \begin{equation} \begin{cases}\label{eq:problemV2} -\Delta v + v = 0 & \text{in } \Omega,\\ \displaystyle{v = u} & \text{on }\Gamma, \end{cases} \end{equation} where $u$ is the solution of (\ref{eq:problemU}). The function $u$ is now involved as a Dirichlet boundary condition and thus, will appear in the function space of $v$ (again, except if one uses a Lagrange multiplier, which is not the case here). To obtain the weak formulation of problem (\ref{eq:problemV2}), we introduce the following function space \ref{eq:WeakFormulationU} $$ H^1_u(\Omega) = \left\{w\in H^1(\Omega) \text{ such that $w|_{\Gamma} = u|_{\Gamma}$, where $u$ is the solution of problem (1)} \right\}. $$ Thus, we have \begin{equation}\label{eq:WeakFormulationV2} \left\{\begin{array}{l} \text{Find } v\in H^1_u(\Omega) \text{ such that, }\\ \displaystyle{\forall v'\in H^1_0(\Omega), \qquad \int_{\Omega} \nabla v\cdot\nabla v' \;{\rm d}\Omega + \int_{\Omega}vv' \;{\rm d}\Omega = 0}, \end{array}\right. \end{equation}

GetDP

In GetDP, a Dirichlet boundary condition is generally imposed through the "Constraint" term, it can be imposed with the help of a Lagrange multiplier. In the second case, the Dirichlet boundary condition is no more "imposed" in the function space but appears in the weak formulation (as a Neumann boundary condition). Thus, the previous case can be used. Here is only considered the first case using the GetDP function "AssignFromResolution". A Resolution dedicated to $u$ must then be created, in this example it will be named AuxiliaryResolution. In GetDP, the procedure can be summarized as follows:

  • Create a constraint with :
Type AssignFromResolution ; Resolution AuxiliaryResolution;
  • Construct only ONE function space that will contain $u$ and at the end $v$ ($u$ will be erased !)
  • Create two Resolution, one for $v$ and one for $u$ :
    • for $v$ : Generate, Solve, Save
    • for $u$ (AuxiliaryResolution) : Generate, Solve, TransfertSolution (do not Save !)

With this, GetDP will ... :

  • Try to solve problem with $v$
  • Need the Dirichlet constraint (that is $u$)
  • Solve problem with $u$
  • Solve problem with $v$

Sometimes it is usefull to save both $u$ and $v$ at the end of the calculation. This can be done by adding an auxiliary problem that "copy" $u$ (see the last paragraph).

Files

There are two files :

Secondpb.geo 
exactly the same as FirstPb.geo
Secondpb.pro 
quite the same as FirstPb.pro

To solve the problem, type in a terminal (in the right directory) :

gmsh SecondPb.geo -2

and then solve the problem with getdp :

getdp SecondPb.pro -solve -pos

and chose the first resolution (MainResolution) or directly

getdp SecondPb.pro -solve MainResolution -pos Map_v
//Caracteristic length of the finite elements (reffinement is also possible after the mesh is built):
lc = 0.05;

// The parameters of the border of the domain :
x_max = 1;
x_min = 0;
y_max= 1;
y_min = 0;

//Creation of the 4 angle points of the domain Omega (=square)
p1 = newp; Point(p1) = {x_min,y_min,0,lc};
p2 = newp; Point(p2) = {x_min,y_max,0,lc};
p3 = newp; Point(p3) = {x_max,y_max,0,lc};
p4 = newp; Point(p4) = {x_max,y_min,0,lc};

//The four edges of the square
L1 = newreg; Line(L1) = {p1,p2};
L2 = newreg; Line(L2) = {p2,p3};
L3 = newreg; Line(L3) = {p3,p4};
L4 = newreg; Line(L4) = {p4,p1};

// Line Loop (= boundary of the square)
Bound = newreg; Line Loop(Bound) = {L1,L2,L3,L4};

//Surface of the square
SurfaceOmega = newreg; Plane Surface(SurfaceOmega) = {Bound};

// To conclude, we define the physical entities, that is "what GetDP could see/use".
// 1 is associtated to Omega
// 2 to Gamma
Physical Surface(1) = {SurfaceOmega};
Physical Line(2) = {L1,L2,L3,L4};
// Do not forget to let a blank line at the end, this could make GMSH crash...

Direct link to file `CoupledProblems/Second/SecondPb.geo'

// Group
//======
Group{
Omega = Region[{1}];
Gama = Region[{2}];
}

// Function
//=========
Function{
C = 5; //constant C in the problem solved by u
}

//Jacobian
//========
Jacobian {
  { Name JVol ;
    Case {
      { Region All ; Jacobian Vol ; }
    }
  }
  { Name JSur ;
    Case {
      { Region All ; Jacobian Sur ; }
    }
  }
  { Name JLin ;
    Case {
      { Region All ; Jacobian Lin ; }
    }
  }
}

//Integration (parameters)
//=======================
Integration {
  { Name I1 ;
    Case {
      { Type Gauss ;
        Case {
          { GeoElement Point ; NumberOfPoints  1 ; }
          { GeoElement Line ; NumberOfPoints  4 ; }
          { GeoElement Triangle ; NumberOfPoints  6 ; }
          { GeoElement Quadrangle ; NumberOfPoints 7 ; }
          { GeoElement Tetrahedron ; NumberOfPoints 15 ; }
          { GeoElement Hexahedron ; NumberOfPoints 34 ; }
        }
      }
    }
  }
}

// Dirichlet Constraint
Constraint{
    {Name DirichletV;
    Case{
        {Region Gama; Type AssignFromResolution; NameOfResolution AuxiliaryResolution; }
    }
    }
}
/*
The constraint will be obtained through the resolution of "AuxiliaryResolution".
This means that GetDP will automatically solve "AuxiliaryResolution" when it will
need the contraint !
*/

//FunctionSpace
//=============
FunctionSpace{
//Space for u AND v !!
	{ Name Hgrad; Type Form0;
    BasisFunction{
      {Name wn; NameOfCoef vn; Function BF_Node;
    Support Region[{Omega, Gama}]; Entity NodesOf[All];}
    }
    //the dirichlet constraint "v = u" on Gamma
    Constraint{
    {NameOfCoef vn; EntityType NodesOf;
     NameOfConstraint DirichletV;}
     }
    }
}
/*
ONLY one function space that will contain "u" and at the end, "v".
*/


//(Weak) Formulations
//==================

Formulation{
// Problem solved by u :
// Delta u + u = C (Omega)
// dn u = 0 (Gamma)
  {Name ProblemU; Type FemEquation;
    Quantity{
      {Name u; Type Local; NameOfSpace Hgrad;}
    }
    Equation{
      Galerkin{ [Dof{Grad u}, {Grad u}];
        In Omega; Jacobian JVol; Integration I1;}
      Galerkin{ [Dof{u}, {u}];
        In Omega; Jacobian JVol; Integration I1;}
      Galerkin{ [-C, {u}];
        In Omega; Jacobian JVol; Integration I1;}
    }
  }

// Coupled problem : "first kind" : 
// DIRICHLET condition on Gamma 
// Delta v + v =0 Omega
// v = u on Gamma
  {Name ProblemV; Type FemEquation;
    Quantity{
    // v is the unknown
      {Name v; Type Local; NameOfSpace Hgrad;}
    }
    Equation{
      Galerkin{ [Dof{Grad v}, {Grad v}];
        In Omega; Jacobian JVol; Integration I1;}

      Galerkin{ [Dof{v}, {v}];
        In Omega; Jacobian JVol; Integration I1;}
    }
  }
  
  
}

// Resolution
//===========

Resolution{
//Main Resolution : the one that will be called when launching getdp
  {Name MainResolution;
    System{
      {Name PbV; NameOfFormulation ProblemV;}
    }
    Operation{
      Generate[PbV]; Solve[PbV]; SaveSolution[PbV];
    }
  }
/*Short explanations : GetDP will :
generate and solve the problem associated to "v" and save "v" in the space H1
However, to compute "v", GetDP need to compute the Dirichlet Contraint, thus
is needs to solve AuxiliaryResolution (bellow) !
*/

// Auxiliary resolution that computes "u"
  {Name AuxiliaryResolution;
    System{
    //System associated to "u" will be transfered to the weak formulation of "v"
      {Name PbU; NameOfFormulation ProblemU; DestinationSystem PbV;}
      {Name PbV; NameOfFormulation ProblemV;}
    }
    Operation{
      Generate[PbU]; Solve[PbU]; TransferSolution[PbU];
    }
  }
/*Short explanations : GetDP will :
1) generate and solve the problem associated to "u"
2) Transfert solution u (to problem associated to "v")
*/
}


//Post Processing
//===============

PostProcessing{
  {Name CoupledProblem; NameOfFormulation ProblemV;
    Quantity{
      {Name v; Value {Local{[{v}];In Omega; Jacobian JVol;}}}
    }
  }
}

//Post Operation
//==============

PostOperation{
  {Name Map_v; NameOfPostProcessing CoupledProblem;
    Operation{
      Print[v, OnElementsOf Omega, File "sol_v.pos"];
    }
  }
}

Direct link to file `CoupledProblems/Second/SecondPb.pro'

Result

Solution v.

Second kind of coupled problem with a save of solution $u$

Sometimes, it can be usefull to save both $u$ and $v$. To achieved this, one can introduce an auxiliary variable $u_{aux}$ that will be a copy of $u$. Here, we proposed to add :

A new FunctionSpace to store $u$
A new weak formulation to copy $u$ into an auxiliary variable $u_{aux}$

The modified .pro file (SecondPbWithSave.pro) can be found below. The .geo file being exactly the same as the previous ones. 

//Caracteristic length of the finite elements (reffinement is also possible after the mesh is built):
lc = 0.05;

// The parameters of the border of the domain :
x_max = 1;
x_min = 0;
y_max= 1;
y_min = 0;

//Creation of the 4 angle points of the domain Omega (=square)
p1 = newp; Point(p1) = {x_min,y_min,0,lc};
p2 = newp; Point(p2) = {x_min,y_max,0,lc};
p3 = newp; Point(p3) = {x_max,y_max,0,lc};
p4 = newp; Point(p4) = {x_max,y_min,0,lc};

//The four edges of the square
L1 = newreg; Line(L1) = {p1,p2};
L2 = newreg; Line(L2) = {p2,p3};
L3 = newreg; Line(L3) = {p3,p4};
L4 = newreg; Line(L4) = {p4,p1};

// Line Loop (= boundary of the square)
Bound = newreg; Line Loop(Bound) = {L1,L2,L3,L4};

//Surface of the square
SurfaceOmega = newreg; Plane Surface(SurfaceOmega) = {Bound};

// To conclude, we define the physical entities, that is "what GetDP could see/use".
// 1 is associtated to Omega
// 2 to Gamma
Physical Surface(1) = {SurfaceOmega};
Physical Line(2) = {L1,L2,L3,L4};
// Do not forget to let a blank line at the end, this could make GMSH crash...

Direct link to file `CoupledProblems/SecondWithSave/SecondPbWithSave.geo'

// Group
//======
Group{
Omega = Region[{1}];
Gama = Region[{2}];
}

// Function
//=========
Function{
C = 5; //constant C in the problem solved by u
}

//Jacobian
//========
Jacobian {
  { Name JVol ;
    Case {
      { Region All ; Jacobian Vol ; }
    }
  }
  { Name JSur ;
    Case {
      { Region All ; Jacobian Sur ; }
    }
  }
  { Name JLin ;
    Case {
      { Region All ; Jacobian Lin ; }
    }
  }
}

//Integration (parameters)
//=======================
Integration {
  { Name I1 ;
    Case {
      { Type Gauss ;
        Case {
          { GeoElement Point ; NumberOfPoints  1 ; }
          { GeoElement Line ; NumberOfPoints  4 ; }
          { GeoElement Triangle ; NumberOfPoints  6 ; }
          { GeoElement Quadrangle ; NumberOfPoints 7 ; }
          { GeoElement Tetrahedron ; NumberOfPoints 15 ; }
          { GeoElement Hexahedron ; NumberOfPoints 34 ; }
        }
      }
    }
  }
}

// Dirichlet Constraint
Constraint{
    {Name DirichletV;
    Case{
        {Region Gama; Type AssignFromResolution; NameOfResolution AuxiliaryResolution; }
    }
    }
}
/*
The constraint will be obtained through the resolution of "AuxiliaryResolution".
This means that GetDP will automatically solve "AuxiliaryResolution" when it will
need the contraint !
*/

//FunctionSpace
//=============
FunctionSpace{
//Space for u
	{ Name Hgrad_u; Type Form0;
    BasisFunction{
      {Name wn; NameOfCoef vn; Function BF_Node;
    Support Region[{Omega, Gama}]; Entity NodesOf[All];}
    }
    }

//Space for u_aux (=copy of u) AND v !!
	{ Name Hgrad_v; Type Form0;
    BasisFunction{
      {Name wn; NameOfCoef vn; Function BF_Node;
    Support Region[{Omega, Gama}]; Entity NodesOf[All];}
    }
    //the dirichlet constraint "v = u" on Gamma
    Constraint{
    {NameOfCoef vn; EntityType NodesOf;
     NameOfConstraint DirichletV;}
     }
    }
}


//(Weak) Formulations
//==================

Formulation{
// Problem solved by u :
// Delta u + u = C (Omega)
// dn u = 0 (Gamma)
  {Name ProblemU; Type FemEquation;
    Quantity{
      {Name u; Type Local; NameOfSpace Hgrad_u;}
    }
    Equation{
      Galerkin{ [Dof{Grad u}, {Grad u}];
        In Omega; Jacobian JVol; Integration I1;}
      Galerkin{ [Dof{u}, {u}];
        In Omega; Jacobian JVol; Integration I1;}
      Galerkin{ [-C, {u}];
        In Omega; Jacobian JVol; Integration I1;}
    }
  }

// Coupled problem : "first kind" : 
// DIRICHLET condition on Gamma 
// Delta v + v =0 Omega
// v = u on Gamma
  {Name ProblemV; Type FemEquation;
    Quantity{
    // v is the unknown
      {Name u; Type Local; NameOfSpace Hgrad_u;}
      {Name v; Type Local; NameOfSpace Hgrad_v;}
    }
    Equation{
      Galerkin{ [Dof{Grad v}, {Grad v}];
        In Omega; Jacobian JVol; Integration I1;}

      Galerkin{ [Dof{v}, {v}];
        In Omega; Jacobian JVol; Integration I1;}
    }
  }
  
  //Copy "u" in "u_aux"
  {Name CopyU; Type FemEquation;
    Quantity{
    // v is the unknown
      {Name u; Type Local; NameOfSpace Hgrad_u;}
      {Name u_aux; Type Local; NameOfSpace Hgrad_v;}
    }
    Equation{
      Galerkin{ [Dof{u_aux}, {u_aux}];
        In Omega; Jacobian JVol; Integration I1;}

      Galerkin{ [-{u}, {u_aux}];
        In Omega; Jacobian JVol; Integration I1;}
    }
  }
  
  
}

// Resolution
//===========

Resolution{
//Main Resolution : the one that will be called when launching getdp
  {Name MainResolution;
    System{
    	{Name PbV; NameOfFormulation ProblemV;}
    }
    Operation{
      Generate[PbV]; Solve[PbV]; SaveSolution[PbV];
    }
  }
/*Short explanations : GetDP will :
Try to compute "v", however, GetDP needs to compute the Dirichlet Contraint
thus to solve AuxiliaryResolution (below) !
*/

// Auxiliary resolution that computes "u"
  {Name AuxiliaryResolution;
    System{
    //System associated to "u" will be transfered to the weak formulation of "v"
      {Name PbU; NameOfFormulation ProblemU;}
      {Name PbUaux; NameOfFormulation CopyU; DestinationSystem PbV;}
      {Name PbV; NameOfFormulation ProblemV;}
    }
    Operation{
      Generate[PbU]; Solve[PbU]; SaveSolution[PbU];
      Generate[PbUaux]; Solve[PbUaux]; TransferSolution[PbUaux];
    }
  }
/*Short explanations : GetDP will :
1) Compute "u"
2) Copy "u" in "uaux"
3) Transfert solution "uaux" (to problem associated to "v")
*/
}


//Post Processing
//===============

PostProcessing{
  {Name CoupledProblem; NameOfFormulation ProblemV;
    Quantity{
      {Name u; Value {Local{[{u}];In Omega; Jacobian JVol;}}}
      {Name v; Value {Local{[{v}];In Omega; Jacobian JVol;}}}
    }
  }
}

//Post Operation
//==============

PostOperation{
  {Name Map_Sol; NameOfPostProcessing CoupledProblem;
    Operation{
      Print[u, OnElementsOf Omega, File "sol_u.pos"];
      Print[v, OnElementsOf Omega, File "sol_v.pos"];
    }
  }
}

Direct link to file `CoupledProblems/SecondWithSave/SecondPbWithSave.pro'

Solution v.

All files

A zipfile containing all files (.geo, .pro, .mesh and .pos) can be downloaded here.

Retrieved from "http://onelab.info/onelab_wiki/index.php?title=Tutorial/Coupled_problems&oldid=7761"