Difference between revisions of "Superconducting wire"
From ONELAB
(→Additional information) |
(→Additional information) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
To run the model, open '''helix.pro''' with Gmsh. | To run the model, open '''helix.pro''' with Gmsh. | ||
| − | The model uses | + | The model uses an [[Magnetodynamics with cohomology conditions#Problem definition|H-formulation]] and the Gmsh cohomology solver <ref name= Pellika2013 /><ref name=Stenvall2014 />. The nonlinear resistivity $\rho=\frac{E_c}{J_c}(\frac{\|\vec{J}\|}{J_c})^{n-1}$ in the superconducting filaments is linearized as in <ref name=Kameni2012 />. The number and layers of superconducting filaments, the twist pitch as well as the radius of the conducting matrix are parametrizable, and the model can be solved both in 2D and in 3D. |
== References == | == References == | ||
Latest revision as of 09:57, 28 October 2015
|
2D and 3D models of superconducting wires.
|
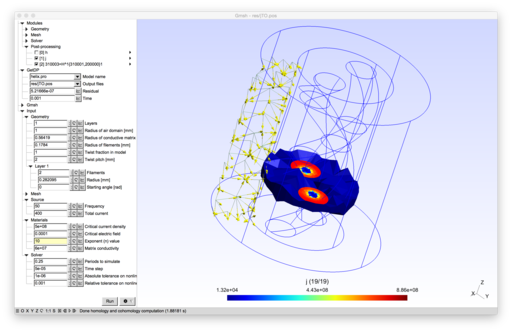 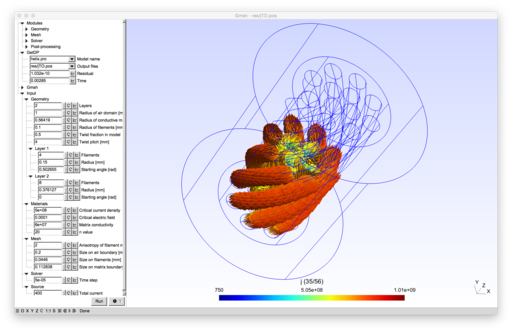
|
|---|
|
Download model archive (superconductors.zip) |
Additional information
To run the model, open helix.pro with Gmsh.
The model uses an H-formulation and the Gmsh cohomology solver [1][2]. The nonlinear resistivity $\rho=\frac{E_c}{J_c}(\frac{\|\vec{J}\|}{J_c})^{n-1}$ in the superconducting filaments is linearized as in [3]. The number and layers of superconducting filaments, the twist pitch as well as the radius of the conducting matrix are parametrizable, and the model can be solved both in 2D and in 3D.
References
- ↑ M. Pellikka, S. Suuriniemi, L. Kettunen and C. Geuzaine, Homology and cohomology computation in finite element modeling. SIAM Journal on Scientific Computing 35(5), pp. 1195-1214, 2013.
- ↑ A. Stenvall, V. Lahtinen and M. Lyly. An H-formulation-based three-dimensional hysteresis loss modelling tool in a simulation including time varying applied field and transport current: the fundamental problem and its solution. Supercond. Sci. Technol. 27 (2014) 104004 (7pp)
- ↑ A. Kameni, J. Lambrechts, J.-F. Remacle, S. Mezani, F. Bouillaut and C. Geuzaine. Discontinuous Galerkin Method for Computing Induced Fields in Superconducting Materials. IEEE Transactions on Magnetics 48(2), pp 591-594, 2012.
|
Model developed by C. Geuzaine, A. Kameni and A. Stenvall.
|

