Difference between revisions of "Acoustic scattering"
| Line 167: | Line 167: | ||
{{GetDPTutorial|Acoustic_scattering/ABC/GMSH_GETDP/Acoustic2D_impenetrable.pro|height=22em}} | {{GetDPTutorial|Acoustic_scattering/ABC/GMSH_GETDP/Acoustic2D_impenetrable.pro|height=22em}} | ||
| − | + | --> | |
| − | + | === Analysis types === | |
| − | |||
| − | |||
| − | |||
| − | + | You can choose to impose Dirichlet or Neumann boundary conditions by selecting the corresponding '''Resolution''' in the GetDP subtree. | |
| − | + | In the same subtree the '''Post-processing''' menu allows you to choose different fields to visualize: | |
| − | + | : (1) '''ud''': Dirichlet, compute the field $u$ and the total field $u + u^{inc}$ and their absolute values | |
| − | + | : (2) '''ud_farfield''': Dirichlet, far field of the scattered field | |
| − | + | : (3) '''ud_traces''': Dirichlet, compute the normal derivative trace of $u$ along $\Gamma$ | |
| − | : (1) ud: Dirichlet, compute the field $u$ and the total field $u + u^{inc}$ and their absolute values | + | : (4) '''un''': same as (1) for a Neumann boundary condition |
| − | : (2) ud_farfield: Dirichlet, far field of the scattered field | + | : (5) '''un_farfield''': same as (2) for a Neumann boundary condition |
| − | : (3) ud_traces: Dirichlet, compute the normal derivative trace of $u$ along $\Gamma$ | + | : (6) '''un_traces''': Neumann, compute the trace of $u$ along $\Gamma$ |
| − | : (4) un: same as (1) for a Neumann boundary condition | + | : (7) '''uinc''': compute the incident field $u^{inc}$ |
| − | : (5) un_farfield: same as (2) for a Neumann boundary condition | ||
| − | : (6) un_traces: Neumann, compute the trace of $u$ along $\Gamma$ | ||
| − | : (7) uinc: compute the incident field $u^{inc}$ | ||
| − | |||
=== Results === | === Results === | ||
Revision as of 10:12, 5 December 2013
|
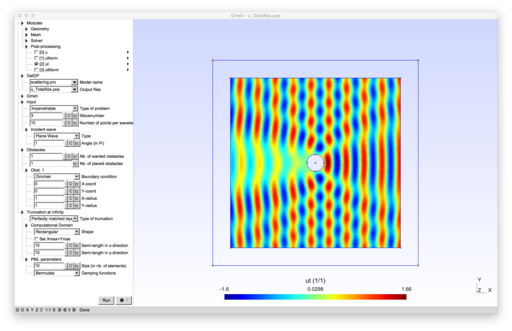
2D model of the scattering of a wave by multiple ellipsoidal obstacles.
|
|
|---|
|
Download model archive (acoustic_scattering.zip) |
Contents
Additional information
To run the model, open scattering.pro with Gmsh.
Scattering problem
Let $\Omega_1^-, \Omega_2^-, \ldots, \Omega_M^-$, be $M$ bounded, disjoint and connected open subset of $\mathbb{R}^2$ such that $\mathbb{R}^2\setminus\overline{\Omega_p^-}$ is connected for $p=1,\ldots,M$. Let $\Omega^- = \bigcup_{p=1}^M\Omega^-_p$ be the domain occupied by the $M$ obstacles and $\Omega^+ = \mathbb{R}^2\setminus\overline{\Omega^-}$ be the connected propagation domain which is also assumed to be connected. Lastly, $\Gamma$ denotes the boundary $\Omega^-$ with a unit outwardly directed normal $\mathbf{n}$.
When the obstacles $\Omega^-$ is illuminated by a time-harmonic incident wave $u^{inc}$, it generates a scattered field $u$, solution of the scattering problem, where $k >0$ is the wavenumber and the time dependence is assumed to be of the form $e^{-ikt}$, \begin{equation}\label{eq:pbu} \begin{cases} \Delta u + k^2 u = 0 & \text{ in } \Omega^+\\ u = -u^{inc} & \text{ on } \Gamma \\ \text{ u outgoing.} & \end{cases} \end{equation} The operator $\Delta$ is the Laplace operator. Here, the boundary condition is a Dirichlet one (sound-soft obstacle), however, a Neumann boundary condition can also be applied (sound-hard scatterer). The outgoing condition stands for the Sommerfeld radiation condition $$ \displaystyle{\lim_{\|\mathbf{x}\| \to \infty} \|\mathbf{x}\|^{(1)/2}\left( \nabla \cdot \frac{\mathbf{x}}{\|\mathbf{x}\|} - iku\right)=0,} $$ where $\|\mathbf{x}\| = \sqrt{x_1^2 + x_2^2}$ is the euclidian norm on $\mathbb{R}^2$.
Problem (\ref{eq:pbu}) admits a unit solution[1]. To solve it numerically using a finite element method, one must truncate the infinit domain $\Omega$. Several methods exist, such as Absorbing Boundary Condition (ABC) [2], Perfectly Matched Layer (PML)[3] [4], Boundary Integral Equation (BIE)[5], $\ldots$ A revue of different technics can be found here[6]. In this example is considered only the case of an ABC, moreover, a simple one (Sommerfeld-like). An implementation of a PML is also proposed on this website. We introduce a fictitious boundary $\Gamma^{\infty}$ surrounding all the scatterers. To simplify, we assume that $\Gamma^{\infty}$ is a disk of radius $R$ and centered on $O = (0,0)$. We denote by $\Omega$ the subset of $\Omega^+$ with boundary $\Gamma^{\infty}\bigcup\Gamma$ (the intersection between the infinite domain $\Omega^+$ and the disk of center $O$ and radius $R$). On the fictitious boundary $\Gamma^{\infty}$ is pluged the ABC, which is here $$ \partial_{\mathbf{n}}u = iku \qquad \text{ on } \Gamma^{\infty}. $$ Note that the normal $\mathbf{n}$ is pointing outside $\Omega$ on $\Gamma^{\infty}$ (and inside on $\Gamma$). The new problem, which approachs the original one (\ref{eq:pbu}), then reads as \begin{equation}\label{eq:pbuABC} \begin{cases} \Delta u + k^2 u = 0 & \text{ in } \Omega\\ u = -u^{inc} & \text{ on } \Gamma \\ \partial_{\mathbf{n}}u = iku & \text{ on }\Gamma^{\infty}. & \end{cases} \end{equation} To simplify, the name $u$ still refers to the solution of the above problem (even it approximates the "real" solution of problem (\ref{eq:pbu})).
Weak formulation
The following sobolev spaces of $H^1(\Omega)$ must first be introduced $$ V_{inc} = \left\{v \in H^1(\Omega) \text{ such that } v|_{\Gamma} = -u_{inc}\right\}, $$ and $$ V_{0} = \left\{v \in H^1(\Omega) \text{ such that } v|_{\Gamma} = 0\right\}. $$ The weak formulation can now be expressed \begin{equation}\label{eq:Diri} \left\{ \begin{array}{l} \displaystyle{\text{Find } u \in V_{inc} \text{ such that}}\\ \displaystyle{\forall u'\in V_{0},\qquad \int_{\Omega}\nabla u \nabla u'\;{\rm d}\Omega - \int_{\Omega}k^2 uu'\;{\rm d}\Omega - \int_{\Gamma^{\infty}}ik u u'\;{\rm d}\Gamma^{\infty} =0.} \end{array}\right. \end{equation}
In the Neumann case, that is $\partial_{\mathbf{n}}u = -\partial_{\mathbf{n}}u_{inc}$ on $\Gamma$, then the weak formulation reads as $$ \left\{ \begin{array}{l} \displaystyle{\text{Find } u \in H^1(\Omega) \text{ such that}}\\ \displaystyle{\forall u'\in H^1(\Omega),\qquad \int_{\Omega}\nabla u \nabla u'\;{\rm d}\Omega - \int_{\Omega}k^2 uu'\;{\rm d}\Omega - \int_{\Gamma^{\infty}}ik u u'\;{\rm d}\Gamma^{\infty} - \int_{\Gamma}\partial_{\mathbf{n}}u_{inc} u'\;{\rm d}\Gamma =0. } \end{array}\right. $$
Remark: the space $V_{inc}$ is not a Banach space but an Hermitian one and $u$ and $u'$ do not belong to the same space. Thus, the weak formulation (\ref{eq:Diri}) is not written in the usual way of finite element method. However, GetDP takes care of the dirichlet boundary condition and thus, in practice, the user will implement equation (\ref{eq:Diri}) directly.
A few words on the far field
In the direction $\boldsymbol{\theta} = (\cos(\theta),\sin(\theta))$, when $\|\mathbf{x}\|$ tends to infinity, the scattered field $u$ has the following behavior $$ u(\|\mathbf{x}\|\boldsymbol{\theta}) = \frac{e^{ik\|\mathbf{x}\|}}{\|\mathbf{x}\|^{1/2}} a(\theta) + O\left(\frac{1}{\|\mathbf{x}\|}\right), $$ where $a(\theta)$ is the far field of $u$ in the direction $\theta$. To compute this with a finite element method, we propose to use the integral representation of $u$ $$ \forall \mathbf{x}\in\Omega^+,\qquad u(\mathbf{x}) = \int_{\Gamma} \partial_{\mathbf{n}}G(\mathbf{x},\mathbf{y}) u|_{\Gamma}(\mathbf{y}) \;{\rm d}\Gamma(\mathbf{y}) - \int_{\Gamma} G(\mathbf{x},\mathbf{y}) \partial_{\mathbf{n}}u|_{\Gamma}(\mathbf{y}) \;{\rm d}\Gamma(\mathbf{y}), $$ where $G(\mathbf{x},\mathbf{y})$ is the Helmholtz Green function, defined in two dimension by $$ \forall \mathbf{x},\mathbf{y}\in\mathbb{R}^2, \mathbf{x}\neq\mathbf{y},\qquad G(\mathbf{x},\mathbf{y}) = \frac{i}{4}H_0^{(1)}(k\|\mathbf{x}-\mathbf{y}\|), $$ which involves the zeroth order Hankel function of first kind $H_0^{(1)}$. Then, the point $\mathbf{x}$ is thrown to "infinity". In practice, $u(\mathbf{x})$ is computed on a circle with a very large radius (e.g. $1000$). The obtained result will then be close to the far field.
Note that, for a Dirichlet boundary condition, we need to compute the normal derivative $\partial_{\mathbf{n}}u$ of $u$ on $\Gamma$. That is why a Region "TrGr" is computed, composed by the elements of $\Omega$ that are connected to $\Gamma$. More information can be found in the Acoustic2D_impenetrable.pro file.
Incident waves
In the following program, two different kind of incident waves are considered.
- The plane wave of direction $\boldsymbol{\beta}=(\cos(\beta),\sin(\beta))$
$$ u^{inc}(\mathbf{x}) = e^{ik(\boldsymbol{\beta}\cdot\mathbf{x})}, $$ where $\boldsymbol{\beta}\cdot\mathbf{x} = x_1\cos(\beta) + x_2\sin(\beta)$ is the usual inner product on $\mathbb{R}^2$. The gradient of the wave (involved for example in a Neumann boundary condition) is given by $$ \nabla u^{inc}(\mathbf{x}) = ike^{ik(\boldsymbol{\beta}\cdot\mathbf{x})}\boldsymbol{\beta} = iku^{inc}(\mathbf{x})\boldsymbol{\beta} $$
- The wave emitted by a point source located on $\mathbf{s} = (s_1,s_2)$.
Obviously, the point $\mathbf{s}$ must be outside $\overline{\Omega^-}$. The incident wave is then the Green function centered on $\mathbf{s}$ : $$ u^{inc}(\mathbf{x}) = \frac{i}{4}H_0^{(1)}(k\|\mathbf{x}-\mathbf{s}\|). $$ Its gradient is then given by $$ \nabla u^{inc}(\mathbf{x}) = -\frac{i}{4}H_1^{(1)}(k\|\mathbf{x}-\mathbf{s}\|) \frac{\mathbf{x}-\mathbf{s}}{\|\mathbf{x}-\mathbf{s}\|}, $$ where $H_1^{(1)}$ is the Hankel function of the first kind and first order. This is due to the fact that the derivative of the Hankel function of order $0$ is the opposite of the Hankel function of order $1$ $$ (H_0^{(1)})' = -H_1^{(1)}. $$
Analysis types
You can choose to impose Dirichlet or Neumann boundary conditions by selecting the corresponding Resolution in the GetDP subtree. In the same subtree the Post-processing menu allows you to choose different fields to visualize:
- (1) ud: Dirichlet, compute the field $u$ and the total field $u + u^{inc}$ and their absolute values
- (2) ud_farfield: Dirichlet, far field of the scattered field
- (3) ud_traces: Dirichlet, compute the normal derivative trace of $u$ along $\Gamma$
- (4) un: same as (1) for a Neumann boundary condition
- (5) un_farfield: same as (2) for a Neumann boundary condition
- (6) un_traces: Neumann, compute the trace of $u$ along $\Gamma$
- (7) uinc: compute the incident field $u^{inc}$
Results
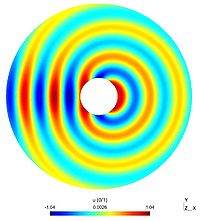
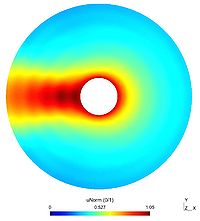
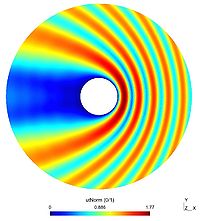
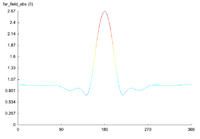
Single scattering
Here is one result obtained with one circular scatterers of radius $2$, with $k=2$ and an incident angle of $\pi$. The first picture depicted the real part of the scattered field $u$, the second one being the absolute value of $u$. The third figure represents the modulus of the total field $u+u_{inc}$ (which is the "physical" field). The last picture shows the far field pattern of the scatterer field.
Multiple scattering
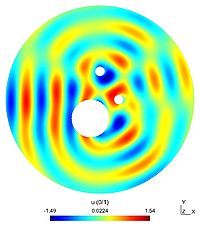
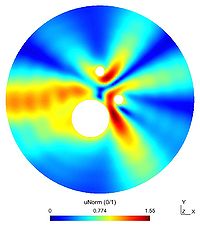
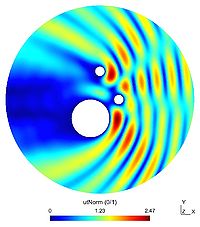
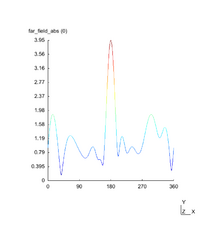
In this example, three obstacles are placed in the domain :
- $(-1,-2)$ with radius $2$
- $(0,3)$ with radius $0.5$
- $(2,0)$ with radius $0.5$
(they are all circular even if it is not a necessarity).
As previously, the first picture shows the real part of the scattered field $u$ and the second the absolute value of $u$. The third figure is a representation of the modulus of the total field $u+u_{inc}$ and the last one shows the far field pattern of the scatterer field.
References
- ↑ D. Colton and R. Kress, Inverse Acoustic and Electromagnetic Scattering Theory, Springer-Verlag, 1998
- ↑ A. Bayliss, M. Gunzburger and E. Turkel, Boundary conditions for the numerical solution of elliptic equations in exterior regions, SIAM Journal on Applied Mathematics, 1982
- ↑ J.-P. Bérenger, A perfectly matched layer for the absorption of electromagnetic waves, Journal of Computational Physics, 1994
- ↑ F. Collino and P. Monk, The perfectly matched layer in curvilinear coordinates, SIAM Journal on Scientific Computing, 1998
- ↑ D. Colton and R. Kress, Integral Equation Methods in Scattering Theory, John Wiley & Sons Inc., 1983
- ↑ X. Antoine, C. Geuzaine and K. Ramdani, Wave Propagation in Periodic Media - Analysis, Numerical Techniques and Practical Applications, Chapter Computational Methods for Multiple Scattering at High Frequency with Applications to Periodic Structures Calculations, Progress in Computational Physics, 2010
|
Model developed by B. Thierry.
|