Difference between revisions of "Bloch modes in periodic waveguides"
From ONELAB
(→Additional information) |
|||
| Line 3: | Line 3: | ||
== Additional information == | == Additional information == | ||
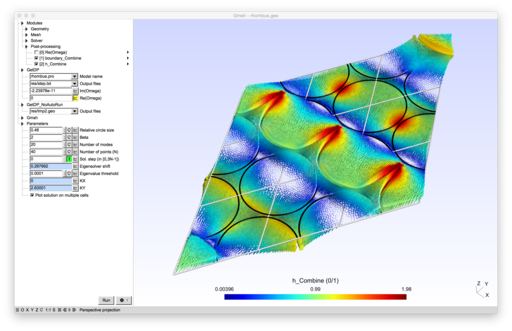
| − | Open '''rhombus.pro''' with Gmsh. The model will automatically compute the | + | Open '''rhombus.pro''' with Gmsh. The model will automatically compute the band diagram of Figure 3.16, p. 152 of Foundations Of Photonic Crystal Fibres<ref name=Zolla2005 />, using a finite element formulation with Floquet-Bloch conditions<ref name=Nicolet2004 />. You can double-click on any point in the diagram to visualize the corresponding eigenmode. |
== References == | == References == | ||
Revision as of 20:41, 25 July 2014
|
Bloch modes in periodic waveguides.
|
|
|---|
|
Download model archive (bloch_periodic_waveguides.zip) |
Additional information
Open rhombus.pro with Gmsh. The model will automatically compute the band diagram of Figure 3.16, p. 152 of Foundations Of Photonic Crystal Fibres[1], using a finite element formulation with Floquet-Bloch conditions[2]. You can double-click on any point in the diagram to visualize the corresponding eigenmode.
References
- ↑ F. Zolla, G. Renversez, A. Nicolet, B. Kuhlmey, S. Guenneau, D. Felbacq, Foundations Of Photonic Crystal Fibres, Imperial College Press, 2005.
- ↑ A. Nicolet, S. Guenneau, C. Geuzaine, F. Zolla, Modelling of electromagnetic waves in periodic media with finite elements, Journal of Computational and Applied Mathematics 168 (1), 321-329, 2004.
|
Model developed by A. Nicolet, F. Zolla and C. Geuzaine.
|

