Difference between revisions of "Diffraction grating"
From ONELAB
| Line 3: | Line 3: | ||
== Additional information == | == Additional information == | ||
| − | To run the model, open ''' | + | To run the model, open '''grating2D.pro''' with Gmsh. |
| + | This model applies to so-called mono-dimensional grating, i.e. structures having one direction of invariance. Various geometries and materials can be handled. The two classical polarization cases, denoted here E// and H//, are addressed. The output consists in a full energy balance of the problem computed from the field maps. For more detailed information and associated bibliography, the curious reader is invited refer to <ref name=Demesy2007 />. | ||
| + | |||
| + | == References == | ||
| + | |||
| + | <references> | ||
| + | |||
| + | <ref name=Demesy2007> G. Demésy, F. Zolla, A. Nicolet, M. Commandré, and C. Fossati, [https://doi.org/10.1364/OE.15.018089 The finite element method as applied to the diffraction by an anisotropic grating], Opt. Express 15, 18089-18102 (2007).</ref> | ||
| + | |||
| + | </references> | ||
{{metamodelfooter|diffraction_grating}} | {{metamodelfooter|diffraction_grating}} | ||
Latest revision as of 20:19, 7 July 2017
|
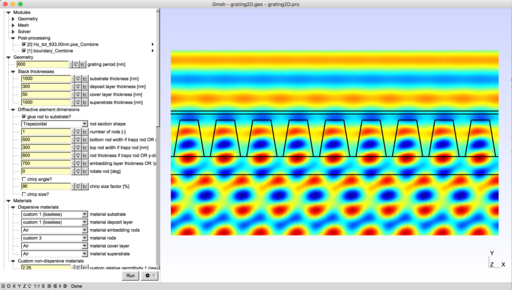
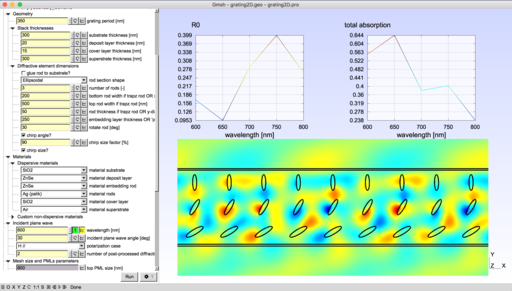
Parametric model of diffraction gratings
|
|
|---|
|
Download model archive (diffraction_grating.zip) |
Additional information
To run the model, open grating2D.pro with Gmsh.
This model applies to so-called mono-dimensional grating, i.e. structures having one direction of invariance. Various geometries and materials can be handled. The two classical polarization cases, denoted here E// and H//, are addressed. The output consists in a full energy balance of the problem computed from the field maps. For more detailed information and associated bibliography, the curious reader is invited refer to [1].
References
- ↑ G. Demésy, F. Zolla, A. Nicolet, M. Commandré, and C. Fossati, The finite element method as applied to the diffraction by an anisotropic grating, Opt. Express 15, 18089-18102 (2007).
|
Models developed by G. Demésy.
|

