Difference between revisions of "Shielding effectiveness"

Latest revision as of 14:06, 10 July 2017

2D and 3D models of cavities for electromagnetic shielding
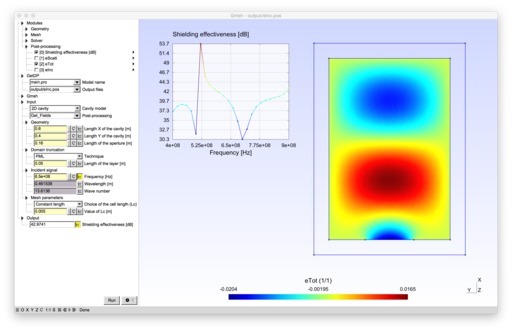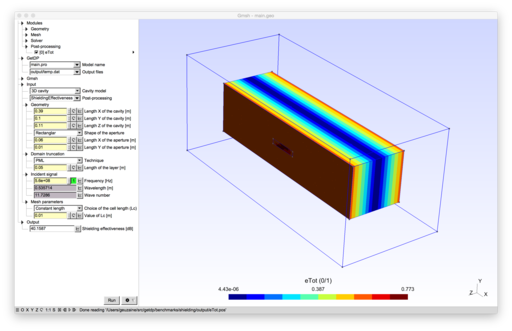
Download model archive (shielding.zip) Browse individual model files and modification history

\(\renewcommand{\vec}[1]{\mathbf{#1}} \newcommand{\Grad}[1]{\mathbf{\text{grad}}\,{#1}} \newcommand{\Curl}[1]{\mathbf{\text{curl}}\,{#1}} \newcommand{\Div}[1]{\text{div}\,{#1}} \newcommand{\Real}[1]{\text{Re}({#1})} \newcommand{\Imag}[1]{\text{Im}({#1})} \newcommand{\pvec}[2]{{#1}\times{#2}} \newcommand{\psca}[2]{{#1}\cdot{#2}} \newcommand{\E}[1]{\,10^{#1}} \newcommand{\Ethree}{{\mathbb{E}^3}} \newcommand{\Etwo}{{\mathbb{E}^2}} \newcommand{\Units}[1]{[\mathrm{#1}]} \)

Introduction

The effectiveness of electromagnetic shields is evaluated in this example. Different academic cavities are considered ^[1][2][3].

To run the model, open main.pro with Gmsh.

Shielding effectiveness

In the time-harmonic context, the ability of a cavity to reduce a signal is quantified by the shielding effectiveness, defined by \begin{equation} 20\:\log_{10} \left|\frac{E^{\text{inc}}}{E^{\text{trans}}}\right| \quad\quad [\text{dB}] \end{equation} where $E^{\text{inc}}$ and $E^{\text{trans}}$ and the amplitudes of the incident wave and the transmitted one, respectively.

References

1. ↑ M. Boubekeur, A. Kameni, L. Pichon, A. Modave and C. Geuzaine, Analysis of transient scattering problems using a discontinuous Galerkin method: application to the shielding effectiveness of enclosures with heterogeneous walls. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 27(3), pp. 626-635, 2014.
2. ↑ J. F. Dawson, M. D. Ganley, A. C. Marvin, S. J. Porter and D. W. P. Thomas, Analytical Formulation for the Shielding Effectiveness of Enclosures with Apertures. IEEE Transactions on Electromagnetic Compatibility, 40(3), pp. 240-248, 1998.
3. ↑ X. Ojeda and L. Pichon, Combining the Finite Element Method and a Padé Approximation for Scattering Analysis Application to Radiated Electromagnetic Compatibility Problems. Journal of Electromagnetic Waves and Applications, 19(40), pp. 1375-1390, 2005.