Difference between revisions of "Tutorial/GetDP basics"

Revision as of 10:17, 3 May 2014

ERROR in secure-include.php: /onelab_files/academic_basics/README.txt does not look like a URL, and doesn't exist as a file.
Download model archive (academic_basics.zip) Browse individual model files

\(\renewcommand{\vec}[1]{\mathbf{#1}} \newcommand{\Grad}[1]{\mathbf{\text{grad}}\,{#1}} \newcommand{\Curl}[1]{\mathbf{\text{curl}}\,{#1}} \newcommand{\Div}[1]{\text{div}\,{#1}} \newcommand{\Real}[1]{\text{Re}({#1})} \newcommand{\Imag}[1]{\text{Im}({#1})} \newcommand{\pvec}[2]{{#1}\times{#2}} \newcommand{\psca}[2]{{#1}\cdot{#2}} \newcommand{\E}[1]{\,10^{#1}} \newcommand{\Ethree}{{\mathbb{E}^3}} \newcommand{\Etwo}{{\mathbb{E}^2}} \newcommand{\Units}[1]{[\mathrm{#1}]} \)

Introduction

This page aims at introducing the resolution of differential problems with GetDP, and provides basic examples. GetDP is a finite element solver for electromagnetism, heat transfer, acoustics and generic PDEs. A resolution is based on a mesh made with GMSH, and a weak formulation written in a GetDP file.

Basis on Gmsh and GetDP

• GMSH file (NAME.geo)

This field is used to build the geometry (the spatial domain). The extension ".geo" is mainly used to design a GMSH file.

• GetDP file (NAME.pro)

This file contains the weak formulation of the problem, and different options for the numerical resolution. The extension ".pro" is associated with GetDP files.

• Auxiliary file (param.geo)

This file contains the index number associated with the geometry. It is load by both the GMSH and the GetDP fiels. This ensures that GMSH and GetDP use the same numbering of the domains.

Meshing with GMSH

Graphical way Launch GMSH and open "NAME.geo" Choose the "mesh" menu and click on "2D" Finally, do not forget to save the mesh by clicking on the "Save" button With a terminal In the right directory, type the command gmsh NAME.geo -algo iso -2 Note that here we chose the isobare algorithm ("iso"). One can also chose the algorithms 'del2d' or 'frontal'. After the mesh is built, a file "NAME.msh" should have been created in the directory.

Solving with GetDP
With a terminal In the right directory, type the command getdp NAME.pro -solve -pos GetDP will then propose the Resolution ("-solve") and the PostOperation ("-pos"). Answer to the two questions. Remarks: The choice can be pre-selected by typing: getdp NAME.pro -solve# -pos# A file called "NAME.pos" is build.

Showing the result with GMSH (post-processing)
Graphical way Launch GMSH and open "NAME.pos" (open $\ldots$) Note that the result is automatically loaded if the solution is made using the GMSH interface. With a terminal In the right directory, type the command: gmsh NAME.pos

First academic examples

Example 1 - Laplace's equation with a Neumann boundary condition

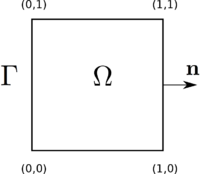
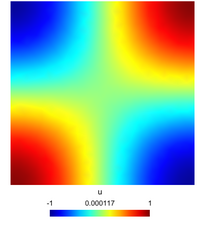
Domain Solution Description of the problem We considered the unit square $\Omega = [0,1]\times[0,1]$ and we seek $u$, solution of the problem \begin{equation} \begin{cases} -\Delta u + u = f & \text{in } \Omega\\ \displaystyle{\frac{\partial u}{\partial \mathbf{n}} = 0} & \text{on }\Gamma \end{cases} \end{equation} where $\displaystyle{\Delta}$ is the Laplace operator $\Gamma$ and $\mathbf{n}$ are the boundary and the unit outward normal of $\Omega$ $f(\mathbf{x})$ is a spatial function defined on $\Omega$ We suppose that the function $f$ is defined by $$ \forall (x,y)\in [0,1]^2,\qquad f(x,y) = (1+2\pi^2)\cos(\pi x)\cos(\pi y). $$ With this choice of $f$, one can easily show that the unique solution of the problem reads as $$ \forall (x,y)\in[0,1]^2, \qquad u(x,y) = \cos(\pi x)\cos(\pi y). $$ Numerical scheme In order to solve the problem with the finite element method, we write the weak formulation of problem: \begin{equation} \left\{\begin{array}{l} \text{Find } u\in H^1(\Omega) \text{ such that, }\\ \displaystyle{\forall v\in H^1(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla v \;{\rm d}\Omega + \int_{\Omega}uv \;{\rm d}\Omega - \int_{\Omega}fv\;{\rm d}\Omega = 0}, \end{array}\right. \end{equation} where $H^1(\Omega)$ is the classical Sobolev space and the functions $v$ are the test functions. Tips for GetDP The functional space $H^1$ is approximated by Form0 in GetDP

Example 2 - Laplace's equation with a Dirichlet boundary condition

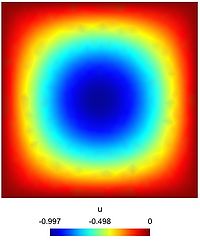
Domain Solution We consider a Laplace equation with a Dirichlet boundary condition. To model this in GetDP, we will introduce a "Constraint". Description of the problem We considered the unit square $\Omega = [0,1]\times[0,1]$ and we seek the function $u$, solution of the following problem \begin{equation} \begin{cases} -\Delta u + u = f & \text{in } \Omega,\\ \displaystyle{u = 0} & \text{on }\Gamma, \end{cases} \end{equation} where $\Gamma = \partial\Omega$ is the boundary of $\Omega$ and $\displaystyle{\Delta = \frac{\partial^2}{\partial x_1^2} + \frac{\partial^2}{\partial x_2^2} }$ is the Laplace operator. To simplify, we suppose that the function $f$ is defined by $$ \forall (x,y)\in [0,1]^2,\qquad f(x,y) = -(1+2\pi^2)\sin(\pi x)\sin(\pi y). $$ As a consequence, the unique solution $u$ of the problem is clearly given by $$ \forall (x,y)\in [0,1]^2, \qquad u(x,y) = -\sin(\pi x)\sin(\pi y). $$ Numerical scheme To solve the problem using the finite element method, we write its weak formulation: \begin{equation} \left\{\begin{array}{l} \text{Find } u\in H^1_0(\Omega) \text{ such that, }\\ \displaystyle{\forall v\in H^1_0(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla v \;{\rm d}\Omega + \int_{\Omega}uv \;{\rm d}\Omega - \int_{\Omega} fv\;{\rm d}\Omega = 0}, \end{array}\right. \end{equation} where the functions $v$ are the test functions and $H^1_0(\Omega) = \left\{ v \in H^1(\Omega) \text{ such that } v|_{\Gamma} = 0\right\}$. Tips for GetDP The functional space $H^1$ is approximated by Form0 in GetDP The homogeneous Dirichlet BC is enforced through the command constraint in the GetDP code

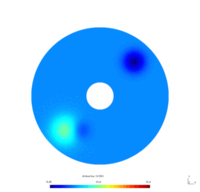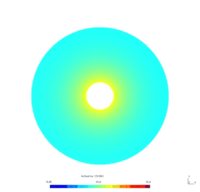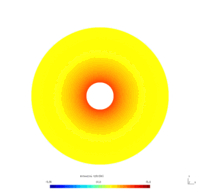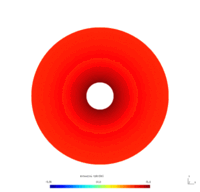
Example 3 - Heat equation with Dirichlet boundary control

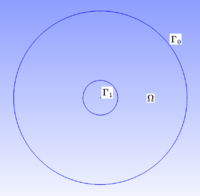
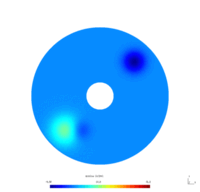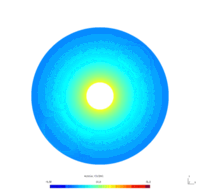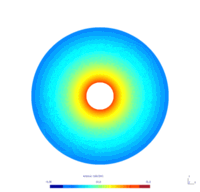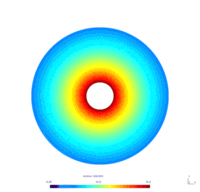
Domain Solution with the Neumann BC on $\Gamma_0$ Solution with the Dirichlet BC on $\Gamma_0$ In this problem, we consider a Heat equation with a Dirichlet control on a part of the boundary, and homogeneous Dirichlet or Neumann condition on the other part. To model this in GetDP, we will introduce a "Constraint" with "TimeFunction". Description of the problem We considered the annulus $\Omega = \mathcal D (0, 1) \setminus \mathcal D (0, 0.2)$. We seek the functions $v_N(x,t)$ and $v_D(x,t)$, respective solutions of the following problems \begin{equation} \begin{cases} \dfrac{\partial}{\partial t} v_N -\Delta v_N = 0 & \forall x \in \Omega, t\geq0\\ \dfrac{\partial v_N}{\partial \mathbf{n}} = 0 & \forall x \in \Gamma_0, t \geq0\\ v_N = u & \forall x \in \Gamma_1, t \geq0. \end{cases} \end{equation} \begin{equation} \begin{cases} \dfrac{\partial}{\partial t} v_D -\Delta v_D = 0 & \forall x \in \Omega, t\geq0\\ v_D = 0 & \forall x \in \Gamma_0, t \geq0\\ v_D = u & \forall x \in \Gamma_1, t \geq0. \end{cases} \end{equation} where $\Gamma_0 = \partial \mathcal D (0, 1)$ is the boundary of $\mathcal D (0, 1)$ $\Gamma_1 = \partial \mathcal D (0, 0.2)$ is the boundary of $\mathcal D (0, 0.2)$ $\Delta$ is the Laplace operator To simplify, we suppose that the control $u$ is defined by $$ \forall (x,y)\in \Gamma_1, t\geq0 \qquad u(x,y,t) = u(t) = 50(1-\exp(-0.5t)). $$ Physically, these problems model the diffusion of the temperature on the annulus over time. The Dirichlet boundary condition models the fact that the temperature on the boundary $\Gamma_0$ is maintained to $0$ (for instance, we put the system in a bowl of ice), as the Neumann boundary condition models the fact that the temperature on the boundary $\Gamma_0$ is let free. Furthermore, the control $u$ corresponds for instance to a thermal resistance, heating the boundary $\Gamma_1$ from $0$ to $50$ degrees. Numerical scheme To solve problems using the finite element method in the space variable, we write their weak formulations: \begin{equation} \left\{\begin{array}{l} \text{Find } v_N\in C^1([0,\infty),\mathcal H_N) \text{ such that, }\\ \displaystyle{\forall \varphi\in \mathcal H_N, t\geq 0, \qquad \int_{\Omega}\dfrac{d v_N}{dt} \varphi \;{\rm d}\Omega + \int_{\Omega} \nabla v_N\cdot\nabla \varphi \;{\rm d}\Omega = 0} \end{array}\right. \end{equation} \begin{equation} \left\{\begin{array}{l} \text{Find } v_D\in C^1([0,\infty), \mathcal H_D) \text{ such that, }\\ \displaystyle{\forall \varphi\in \mathcal H_D, t\geq0, \qquad \int_{\Omega}\dfrac{d v_D}{dt} \varphi \;{\rm d}\Omega + \int_{\Omega} \nabla v_D\cdot\nabla \varphi \;{\rm d}\Omega = 0}, \end{array}\right. \end{equation} where $\mathcal H_N = \{w \in H^1(\Omega) \mid w = u \text{ on } \Gamma_1 \}$ $\mathcal H_D = \{w \in H^1(\Omega) \mid w = 0 \text{ on } \Gamma_0, \; w = u \text{ on } \Gamma_1 \}$ the functions $\varphi$ are the test functions Tips for GetDP In the Formulation group, the DtDof keyword specifies the derivative in time in the weak formulation. In the Resolution group, the TimeLoopTheta keyword indicates that a finite difference time $\theta$-scheme is needed.