Difference between revisions of "Superconducting wire"
From ONELAB
(→Additional information) |
(→Additional information) |
||
| Line 5: | Line 5: | ||
To run the model, open '''helix.pro''' with Gmsh. | To run the model, open '''helix.pro''' with Gmsh. | ||
| − | The model uses a [[Magnetodynamics with cohomology conditions#Problem definition| | + | The model uses a [[Magnetodynamics with cohomology conditions#Problem definition|H-formulation]] and the Gmsh cohomology solver <ref name= Pellika2013 /><ref name=Stenvall2014 />. The nonlinear resistivity $\rho=\frac{E_c}{J_c}(\frac{\|\vec{J}\|}{J_c})^{n-1}$ in the superconducting filaments is linearized as in <ref name=Kameni2012 />. |
== References == | == References == | ||
Revision as of 09:54, 28 October 2015
|
2D and 3D models of superconducting wires.
|
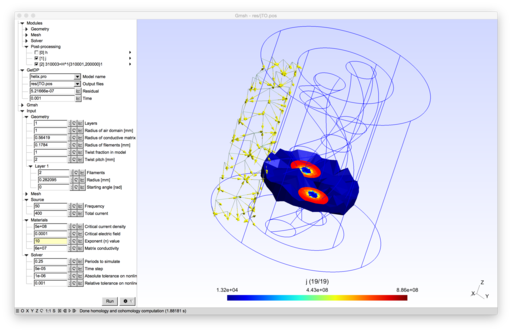 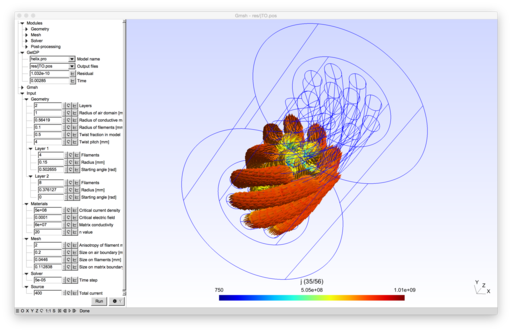
|
|---|
|
Download model archive (superconductors.zip) |
Additional information
To run the model, open helix.pro with Gmsh.
The model uses a H-formulation and the Gmsh cohomology solver [1][2]. The nonlinear resistivity $\rho=\frac{E_c}{J_c}(\frac{\|\vec{J}\|}{J_c})^{n-1}$ in the superconducting filaments is linearized as in [3].
References
- ↑ M. Pellikka, S. Suuriniemi, L. Kettunen and C. Geuzaine, Homology and cohomology computation in finite element modeling. SIAM Journal on Scientific Computing 35(5), pp. 1195-1214, 2013.
- ↑ A. Stenvall, V. Lahtinen and M. Lyly. An H-formulation-based three-dimensional hysteresis loss modelling tool in a simulation including time varying applied field and transport current: the fundamental problem and its solution. Supercond. Sci. Technol. 27 (2014) 104004 (7pp)
- ↑ A. Kameni, J. Lambrechts, J.-F. Remacle, S. Mezani, F. Bouillaut and C. Geuzaine. Discontinuous Galerkin Method for Computing Induced Fields in Superconducting Materials. IEEE Transactions on Magnetics 48(2), pp 591-594, 2012.
|
Model developed by C. Geuzaine, A. Kameni and A. Stenvall.
|

