Tutorial/Laplace equation with Neumann boundary condition
Contents
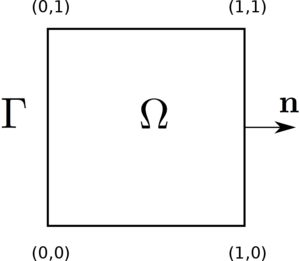
The considered problem
We propose here to solve a first very simple academic example with GMSH and GetDP. We considered the unit square $\Omega$ with boundary $\Gamma$ and unit outward normal $\mathbf{n}$. We seek $u$, solution of the following problem \begin{equation} \begin{cases}\label{eq:problemU} \Delta u + u = f & \text{in } \Omega\\ \displaystyle{\frac{\partial u}{\partial \mathbf{n}} = 0} & \text{on }\Gamma, \end{cases} \end{equation} where the function $f$ is defined by $$ \forall x,y\in [0,1]^2,\qquad f(x,y) = (1+2\pi^2)\cos(\pi x)\cos(\pi y). $$ One can easily show that the unique solution of the problem \eqref{eq:problemU} is $$ \forall x,y\in[0,1]^2, \qquad u(x,y) = \cos(\pi x)\cos(\pi y). $$ In order to solve problem \eqref{eq:problemU} with the finite elements method, we write the weak formulation of the probleme \eqref{eq:problemU}: \begin{equation}\label{eq:WeakFormulation} \left\{\begin{array}{l} \text{Find } u\in H^1(\Omega) \text{ such that, }\\ \displaystyle{\forall v\in H^1(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla v \;{\rm d}\Omega + \int_{\Omega}uv \;{\rm d}\Omega - \int_{\Omega}fv\;{\rm d}\Omega = 0}, \end{array}\right. \end{equation} where $H^1(\Omega)$ is the classical Sobolev space and the functions $v$ are the test functions.
Outline of the program
We give here a (very) detailled solution. Our solution is composed by 3 different files. - LaplacianNeumann.geo : GMSH file, used to build the domain (the square). The extension ".geo" is mainly used to design a GMSH file - LaplacianNeumann.pro : GetDP file, contains the weak formulation \eqref{eq:WeakFormulation} of the problem \eqref{eq:problemU}. The extension ".pro" is associated with GetDP files. - data.geo : this (auxiliary) file contains the index number associated with the geometry. It is used to ensure that GMSH and GetDP have the same numbering of the domains.
param.geo: the auxiliary file
// File "param.geo" //Numbers that caracterise the interior of the square (Omega) and its boundary (Gama): Omega = 1000; // Three remarks on these numbers : // - They are arbitrary choosen. // - They are placed in a separated file to be readable by both GMSH and GetDP. // - "Gamma" is a special word used by GMSH/GetDP, that is why the boundary is named "Gama", with one "m"... // Do not forget to let a blank line at the end, this could make GMSH crash...
Direct link to file `getdp/LaplacianNeumann/GMSH_GETDP/param.geo'
LaplacianNeumann.geo: creation of the geometry with GMSH
// File "LaplacianNeumann.geo".
// We include the file containing the numbering of the geometry.
// This is usefull at the end of this file, and used to "synchronise" GMSH and GetDP
Include "param.geo";
//Caracteristic length of the finite elements (reffinement is also possible after the mesh is built):
lc = 0.05;
// This parameter could be placed for instance in "param.geo", to separate more easyly the geometry
// and the discretization parameters.
// The parameters of the border of the domain :
x_max = 1;
x_min = 0;
y_max= 1;
y_min = 0;
//Creation of the 4 angle points of the domain Omega (=square)
p1 = newp; Point(p1) = {x_min,y_min,0,lc};
p2 = newp; Point(p2) = {x_min,y_max,0,lc};
p3 = newp; Point(p3) = {x_max,y_max,0,lc};
p4 = newp; Point(p4) = {x_max,y_min,0,lc};
// Remarks:
// -"newp" is a GMSH function that give the first available number for describing a point.
// For any other entity, like Line, Surface, etc. We recommand the use of "newreg" (see below).
// - By default, GMSH create a 3D domain. The z-coordinate must always be precised.
//The four edges of the square
L1 = newreg; Line(L1) = {p1,p2};
L2 = newreg; Line(L2) = {p2,p3};
L3 = newreg; Line(L3) = {p3,p4};
L4 = newreg; Line(L4) = {p4,p1};
// Line Loop (= boundary of the square)
Bound = newreg; Line Loop(Bound) = {L1,L2,L3,L4};
//Surface of the square
SurfaceOmega = newreg; Plane Surface(SurfaceOmega) = {Bound};
// To conclude, we define the physical entities, that is "what GetDP could see/use".
// "Omega" is a number imported from the file "param.geo".
Physical Surface(Omega) = {SurfaceOmega};
// Do not forget to let a blank line at the end, this could make GMSH crash...
Direct link to file `getdp/LaplacianNeumann/GMSH_GETDP/LaplacianNeumann.geo'
LaplacianNeumann.pro: weak formulation
// File LaplacianNeumann.pro
// As in the .geo file, we include the file containing the numbering of the geometry.
Include "param.geo";
// Group
//======
//We now build the "Groups", that is, the geometrical entities, the different domains of computation.
//Here we only need the interior of the open domain Omega
Group{
Omega = Region[{Omega}];
}
// Function
//=========
Function{
// Pi is a special value in GetDp (=3.1415...)
Coef = Pi;
// Definition of the source function f(x,y)
f[] = (1+2*Coef*Coef)*Cos[Coef*X[]]*Cos[Coef*Y[]];
}
/*
Remark:
- the argument (as "x" and "y") are not writen between the bracket [].
Indeed, between the bracket is writen the domain of definition of the function.
- The argument "x" and "y" are here designed by the GetDP inner functions X[] and Y[], which give
respectively the x-coordinate and the y-coordinate of a considered point.
- To define a function globaly (i.e: not only on a subdomain), we write:
f[] = ...
- In our example, we could also have written
f[Omega] = (1+2*Coef*Coef)*Cos[Coef*X[]]*Cos[Coef*Y[]];
*/
//Jacobian
//========
Jacobian {
{ Name JVol ;
Case {
{ Region All ; Jacobian Vol ; }
}
}
{ Name JSur ;
Case {
{ Region All ; Jacobian Sur ; }
}
}
{ Name JLin ;
Case {
{ Region All ; Jacobian Lin ; }
}
}
}
/*
Remark: roughly speacking, we make use of...:
- Jacobian "Vol" as far as the integration domain is of same dimension than the problem (e.g: calculation in a 3D domain, in a 3D problem,
a 2D domain (surface) in a 2 problem, a 1D domain (line) in a 1D problem)
- Jacobian "Sur" when the domain of integration has one dimension less than the global problem (e.g:
calculation on a surface (2D) in a 3D problem, calculation on a line (1D) in a 2D problem).
- Jacobian "Lin" when the domain of integration has 2 dimensions less than the problem. That is,
for example, a calculation on a line (1D) in a 3D problem.
- Here, we just have define some Jacobian, you will see later that we just use the Jacobian "JVol"
*/
//Integration (parameters)
//=======================
Integration {
{ Name I1 ;
Case {
{ Type Gauss ;
Case {
{ GeoElement Point ; NumberOfPoints 1 ; }
{ GeoElement Line ; NumberOfPoints 4 ; }
{ GeoElement Triangle ; NumberOfPoints 6 ; }
{ GeoElement Quadrangle ; NumberOfPoints 7 ; }
{ GeoElement Tetrahedron ; NumberOfPoints 15 ; }
{ GeoElement Hexahedron ; NumberOfPoints 34 ; }
}
}
}
}
}
// There is no Constrain because of the Neumann boundary condition
// We go directly to the FuntionSpace
//FunctionSpace
//=============
FunctionSpace{
{ Name Vh; Type Form0;
BasisFunction{
{Name wn; NameOfCoef vn; Function BF_Node;
Support Omega; Entity NodesOf[All];}
}
}
}
/*
Explanation:
The space of approximation is called "Vh".
Its type is "Form0", that means "scalar".
The basis functions are called "wn", and the associated coefficients "vn".
In other words, a function "v" of "Vh" can be written as
v(x,y) = sum_{n} vn.wn(x,y)
The functions "wn" are nodale functions P1 ("BF_Node"), supported on the domain Omega ("Support Omega").
*/
//(Weak) Formulation
//==================
Formulation{
{Name LaplacianNeumann; Type FemEquation;
// We decided to call the formulation "LaplacianNeumann".
// Its type is "FemEquation" ("Finite Element Method")
Quantity{
{Name u; Type Local; NameOfSpace Vh;}
}
// Here, we introduce a quantity "u", which belongs to the function space Vh, defined above.
Equation{
Galerkin{ [Dof{Grad u}, {Grad u}];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ Dof{u}, {u}];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [-f[], {u}];
In Omega; Jacobian JVol; Integration I1;}
}
}
}
/*
The variationnal formulation is written between the acolades {}, after "Equation".
Let us first give some vocabulary:
- "Galerkin" : GetDP syntaxic word. This could be translated mathematicaly by "integration" (see below)
- Dof{u}: "Degree Of Freedom". This is used to specify that the quantity is the unknown.
If "Dof" is not written, then "u" is seen as a test function and not as the unknown.
(Be carreful, the unknown and the test functions has the same name in GetDP !
The "Dof" is here to distinguish the unknown to the test-functions)
Now, let us detail the program written between the acolades {}, :
Galerkin{ [Dof{Grad u}, {Grad u}];
In Omega; Jacobian JVol; Integration Int;}
This could be translated mathematicaly by :
Integration on "Omega" of Grad(u).Grad(v)
where "u" is the unknown and "v" a test function.
Note the use of the Jacobian JVol(2D problem and integration on a 2D domain).
Moreover the number of integrations point is given in "I1" (see above "Integration").
The total variationnal formulation can be read as :
search "Dof{u}" in V_h such that, for every "{u}" in V_h,
\int_{\Omega} Grad( Dof{u}) . Grad( {u}) d\Omega + \int_{\Omega} Dof{u}.{u} d\Omega - ...
... - \int_{\Omega} f.{u} d\Omega = 0
(this is exactly the weak formulation of our problem !)
Remarks:
- Between two "Galerkin", a positive sign "+" is implicitly written
- The sum of all integrals "Galerkin" is equal to 0 (do not forget the "minus" sign of the right hand side)
- Why do we use a volumic jacobian even in a 2D problem? The problem is a 2 dimensional problem and
the integral is defined on a 2D domain (Omega). If the integral was writen on, e.g, the boundary,
then the Jacobian "Jsur" would have been used.
*/
// Resolution (of the problem)
//============================
Resolution{
{Name LaplacianNeumann;
// We chose the name LaplacianNeumann for the resolution
// Remark: in GetDP, every entity has a name. The same same can be used for different entities but of different kind, of course
// Here we chose the same name as the formulation, but this is just a choice, no obligation !
System{
{Name Syst; NameOfFormulation LaplacianNeumann;}
}
// A system is linked to a weak formulation
// Here, we only have one weak formulation, which is "LaplacianNeumann"
Operation{
Generate[Syst]; Solve[Syst]; SaveSolution[Syst];
}
/* When we launch GetDP, the program will ask the user to chose a Resolution.
When calling the Resolution "LaplacianNeumann", GetDP will...
- Generate the system
- Solve the system
- Save the solution
Note that GetDP respects the order of the operation !
*/
}
}
//Post Processing
//===============
PostProcessing{
{Name LaplacianNeumann; NameOfFormulation LaplacianNeumann;
Quantity{
{Name u; Value {Local{[{u}];In Omega;Jacobian JVol;}}}
}
}
}
/*
The name of the PostProcessing is LaplacianNeumann.
It call the weak formulation LaplacianNeumann, then take the solution "u" and compute it on all the domain Omega, by the operation:
Value {Local{[{u}];In Carre; Jacobian JVol;}}}
This means that "u" is the interpolate of the solution "Dof{u}" computed in the weak formulation "LaplacianNeumann"
Remark: Again, we chose the same name, but this is just a choice, this has no influence on GetDP resolution.
*/
//Post Operation
//==============
PostOperation{
{Name Map_u; NameOfPostProcessing LaplacianNeumann;
Operation{
Print[u, OnElementsOf Omega, File "u_Neumann.pos"];
}
}
}
/*
The only PostOperation we write is to display "u" introduced in the PostProcessing.
This PostOperation is called "Map_u".
When launching GetDP, it will ask the user to chose :
- the Resolution
- the PostOperation
*/Direct link to file `getdp/LaplacianNeumann/GMSH_GETDP/LaplacianNeumann.pro'
Mesh
Here is an example of a mesh of $\Omega$
The associated file "LaplacianNeumann.msh" can be downloaded here:
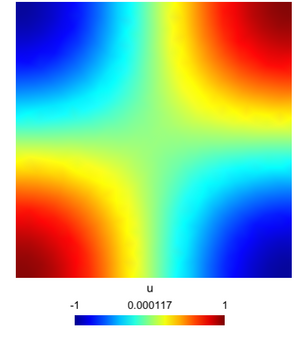
Solution
Finally, we obtain the solution $u$
The .pos file can also be downloaded here: