Domain decomposition methods for waves

From ONELAB
Jump to: navigation, search

Optimized Schwarz domain decomposition methods for time-harmonic wave problems

Download model archive (ddm_wave_simple.zip)
Browse individual model files

Introduction

To run the models, open main.pro with Gmsh. (This is for demonstration uses only. For actual, parallel computations, you should compile GetDP and Gmsh with MPI support: see GetDDM).

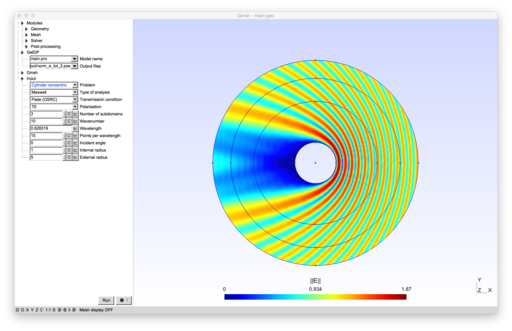
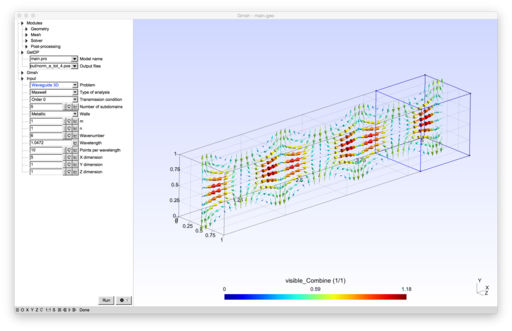
The formulations implement non-overlapping Schwarz domain decomposition methods for the Helmholtz equation and for the time-harmonic Maxwell system. Several families of transmission conditions are implemented: zeroth- and second-order optimized conditions[1][2][3][4][5][6], as well as new Padé-localized square-root conditions[7][8].

References

  1. ↑ B. Després, Méthodes de Décomposition de Domaine pour les Problèmes de Propagation d'Ondes en Régime Harmonique. Le Théorème de Borg pour l'Equation de Hill Vectorielle, PhD Thesis, Paris VI University, France, 1991.
  2. ↑ B. Després, P. Joly and J. Roberts, A domain decomposition method for the harmonic Maxwell equations, Iterative methods in linear algebra (Brussels, 1991), pp. 475-484, North-Holland, 1992.
  3. ↑ M. Gander, F. Magoulès and F. Nataf, Optimized Schwarz methods without overlap for the Helmholtz equation}, SIAM Journal on Scientific Computing, 24(1), pp. 38-60, 2002.
  4. ↑ V. Dolean, M. Gander and L. Gerardo-Giorda, Optimized Schwarz methods for Maxwell's equations, SIAM Journal on Scientific Computing, 31(3), pp. 2193-2213, 2009.
  5. ↑ A. Bendali and Y. Boubendir, Non-Overlapping Domain Decomposition Method for a Nodal Finite Element Method, Numerische Mathematik 103(4), pp.515-537, (2006).
  6. ↑ V. Rawat and J.-F. Lee, Nonoverlapping Domain Decomposition with Second Order Transmission Condition for the Time-Harmonic Maxwell's Equations, SIAM Journal on Scientific Computing, 32(6), pp. 3584-3603, 2010.
  7. ↑ Y. Boubendir, X. Antoine, C. Geuzaine. A quasi-optimal non-overlapping domain decomposition algorithm for the Helmholtz equation. Journal of Computational Physics 231 (2), 262-280, 2012.
  8. ↑ M. El Bouajaji, X. Antoine, C. Geuzaine. Approximate local magnetic-to-electric surface operators for time-harmonic Maxwell’s equations, Journal of Computational Physics, accepted for publication, 2014.


Models developed by X. Antoine, Y. Boubendir, M. El Bouajaji, D. Colignon, C. Geuzaine, N. Marsic, B. Thierry, S. Tournier and A. Vion. This work was funded in part by the Belgian Science Policy (IAP P6/21 and P7/02), the Belgian French Community (ARC 09/14-02), the Walloon Region (WIST3 No 1017086 ONELAB and ALIZEES), the Agence Nationale pour la Recherche (ANR-09-BLAN-0057-01 MicroWave) and the EADS Foundation (grant 089-1009-1006 High-BRID).

Retrieved from "http://onelab.info/onelab_wiki/index.php?title=Domain_decomposition_methods_for_waves&oldid=7467"