Difference between revisions of "Electrostatics template"

Revision as of 17:45, 5 March 2016

\(\renewcommand{\vec}[1]{\mathbf{#1}} \newcommand{\Grad}[1]{\mathbf{\text{grad}}\,{#1}} \newcommand{\Curl}[1]{\mathbf{\text{curl}}\,{#1}} \newcommand{\Div}[1]{\text{div}\,{#1}} \newcommand{\Real}[1]{\text{Re}({#1})} \newcommand{\Imag}[1]{\text{Im}({#1})} \newcommand{\pvec}[2]{{#1}\times{#2}} \newcommand{\psca}[2]{{#1}\cdot{#2}} \newcommand{\E}[1]{\,10^{#1}} \newcommand{\Ethree}{{\mathbb{E}^3}} \newcommand{\Etwo}{{\mathbb{E}^2}} \newcommand{\Units}[1]{[\mathrm{#1}]} \)The Electrostatics.pro template focuses on one of the simplest electromagnetic problem: the determination of the distribution of the electric field $\vec{e}$ $\Units{V/m}$ due to static (non-varying, in both space and time) electric charge densities $\rho$ $\Units{C/m^3}$ and/or levels of electric potential $v$ $\text[V]$. This is called an electrostatic problem, or simply electrostatics.

• Download the templates (they are also directly available in the ONELAB bundle)
• Create a geometry with Gmsh, or open an existing geometry
• File/Merge the Electrostatics.pro template
• For each physical group in the model, you will be asked to select the material, sources or boundary conditions

Every time you run your model, the ONELAB database is saved to disk (you can later reload it using the gear menu). An flattened problem file containing the GetDP definitions is also saved in case you want to edit it manually later on.

Governing equations

The equations describing electrostatics are obtained by dropping the terms with time derivatives (since we only consider static phenomena) in Maxwell's equations. The equations involving the electric and magnetic quantities (the electric field $\vec{e}$ and the electric displacement $\vec{d}$ on one side, the magnetic field $\vec{h}$ and the magnetic induction $\vec{b}$ on the other) then become decoupled and in order to determine the electric field we can thus only consider: \begin{align} \Curl{\vec{e}} &= 0 , \label{eq:curle}\\ \Div{\vec{d}} &= \rho , \label{eq:divd} \end{align} together with the dielectric constitutive law \begin{equation} \vec{d} = \epsilon \vec{e} + \vec{p}_e , \label{eq:de} \end{equation} where the charge density $\rho$ and the source polarization $\vec{p}_e$ are given (see Maxwell's equations for additional details).

Scalar electric potential

Since $\Curl{\vec{e}} = 0$, the electric field can be derived from a scalar potential (the electric scalar potential $v$, whose MKSA unit is the Volt $\Units{V}$) such that \begin{equation} \vec{e} = - \Grad{v} . \label{eq:v} \end{equation}

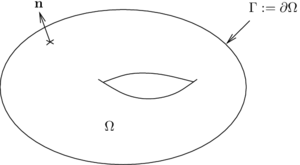
Introducing \eqref{eq:v} and \eqref{eq:de} in \eqref{eq:divd}, we obtain \begin{equation}\label{eq:elesta} -\Div{\epsilon\,\Grad{v}} = \rho . \end{equation} Our goal is to solve this equation in a bounded open set $\Omega$ of the oriented Euclidean space $\Ethree$. Note that if $\epsilon$ is a constant, \eqref{eq:elesta} reduces to Poisson's equation: $\Delta\,v=-\rho/\epsilon$.

Weak formulation

Domain and its boundary.

Let us skip all the mathematical details related to the conditions for the existence and uniqueness of the solution to this problem and focus instead on reformulating of the problem in order to solve it using the finite element method with GetDP. In order to do this, we need to transform the original partial differential equation into a so-called weak formulation. This weak formulation is obtained by testing equation \eqref{eq:elesta} with a series of functions, which means taking the scalar product of the equation with these test functions. Mathematically, one can show that \eqref{eq:elesta} is equivalent to finding the solution $v\in H^1(\Omega)$ (we will come back to what this means shortly) such that \begin{equation}\label{eq:elesta_weak} - \int_\Omega (\Div{\epsilon\,\Grad{v}}) \,v' \,d\Omega = \int_\Omega \rho \,v' \,d\Omega ,\quad \forall v' \in H^1_0(\Omega). \end{equation} This is the weak formulation of \eqref{eq:elesta}, where $H^1(\Omega)$ and $H^1_0(\Omega)$ are Sobolev spaces of square integrable functions whose derivatives are also square integrable. In addition, functions in $H^1_0(\Omega)$ have zero value on the boundary of the domain $\Omega$. The scalar product used here is the standard $L^2$ scalar product \begin{equation} (u,v)_\Omega = \int_\Omega u v \, d\Omega \end{equation} and we will usually thus write \eqref{eq:elesta_weak} in a more compact form as: \begin{equation}\label{eq:elesta_weak2} - (\Div{\epsilon\,\Grad{v}} , v')_\Omega = (\rho , v')_\Omega ,\quad \forall v' \in H^1_0(\Omega). \end{equation}

Setting aside the technical details about Sobolev spaces, what \eqref{eq:elesta_weak2} means is: solving the original equation is equivalent to solving an infinity of scalar equations obtained by taking the scalar product of the original equation with appropriately chosen test functions. We do have an infinity of scalar equations since we must test with each $v' \in H^1_0(\Omega)$, and $H^1_0(\Omega)$ is a vector space of infinite dimension. It is advantageous to integrate the left-hand side of \eqref{eq:elesta_weak2} by parts, which symmetrizes it and reduces the order of the differential operator applied to $v$. Applying Green's first identity, our weak formulation then becomes: Find $v\in H^1(\Omega)$ such that: \begin{equation}\label{eq:elesta_weak3} (\epsilon\,\Grad{v} , \Grad{v'} )_\Omega = (\rho , v')_\Omega ,\quad \forall v' \in H^1_0(\Omega). \end{equation} Note that the boundary term $(\vec{n}\cdot\Grad{v} , v' )_{\partial\Omega}$ that arises through integration by parts vanishes here since we chose $v'\in H^1_0(\Omega)$, which implies that $v'\equiv 0$ on the boundary $\partial\Omega$ of the domain $\Omega$.

Implementation in GetDP

GetDP uses weak formulations such as \eqref{eq:elesta_weak3} to define the problems it can solve. Solving an electrostatic problem in GetDP thus amounts to transcribe \eqref{eq:elesta_weak3} into GetDP's own language, which is what is done in Electrostatics.pro