Difference between revisions of "Tutorial/Laplace equation with Dirichlet boundary condition"
(→The considered problem) |
(→TEST) |
||
| Line 51: | Line 51: | ||
{{tutorial|getdp/LaplacianDirichlet/GMSH_GETDP/LaplacianDirichlet.pro|height=22em}} | {{tutorial|getdp/LaplacianDirichlet/GMSH_GETDP/LaplacianDirichlet.pro|height=22em}} | ||
| − | == | + | == Result == |
| − | |||
| − | |||
Revision as of 11:37, 23 September 2011
Contents
The considered problem
In this problem, we consider a Laplace equation, as in that example, except that the boundary condition is here of Dirichlet type. To model this in GetDP, we will introduce a "Constraint". We assume that the reader has already study the previous example.
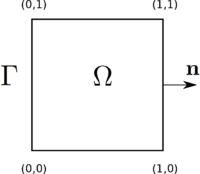
As in the example with a Neumann boundary condition, we considered the unit square $\Omega = [0,1]\times[0,1]$ and the unknown function $u$ solves the following problem \begin{equation} \begin{cases}\label{eq:problemU} \Delta u + u = f & \text{in } \Omega,\\ \displaystyle{u = 0} & \text{on }\Gamma, \end{cases} \end{equation} where $\Gamma = \partial\Omega$ is the boundary of $\Omega$ and $\displaystyle{\Delta = \frac{\partial^2}{\partial x_1^2} + \frac{\partial^2}{\partial x_2^2} }$ is the Laplacian operator.
To simplify, we suppose that the function $f$ is defined by $$ \forall (x,y)\in [0,1]^2,\qquad f(x,y) = (1+2\pi^2)\cos(\pi x)\cos(\pi y). $$ As a consequence, the unique solution $u$ of the problem \eqref{eq:problemU} is clearly given by $$ \forall (x,y)\in [0,1]^2, \qquad u(x,y) = \cos(\pi x)\cos(\pi y). $$ In order to solve problem \eqref{eq:problemU} with the finite elements method, we write the weak formulation of problem \eqref{eq:problemU}: \begin{equation}\label{eq:WeakFormulation} \left\{\begin{array}{l} \text{Find } u\in H^1_0(\Omega) \text{ such that, }\\ \displaystyle{\forall v\in H^1_0(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla v \;{\rm d}\Omega + \int_{\Omega}uv \;{\rm d}\Omega = 0}, \end{array}\right. \end{equation} where the functions $v$ are the test functions and $H^1_0(\Omega) = \left\{ v \in H^1(\Omega) \text{ such that } v|_{\Gamma} = 0\right\}$.
Outline of the program
The proposed solution is composed by 3 different files:
- param.geo
- Auxiliary file that contains the index number associated with the geometry.
- LaplacianNeumann.geo
- GMSH file, used to build both the square $\Omega$ and its boundary $\Gamma$. Except for the building of $\Gamma$, this file is the same as in the previous example.
- LaplacianNeumann.pro
- GetDP file, contains the weak formulation \eqref{eq:WeakFormulation} of the problem \eqref{eq:problemU}. The main difference between this example and the Neumann case is the addition of the Constraint part, which is located in this GetDP file.
param.geo: the auxiliary file
// File "param.geo" //Numbers that caracterise the interior of the square (Omega) and its boundary (Gama): Omega = 1000; Gama = 1001; // Three remarks on these numbers : // - They are arbitrary choosen. // - They are placed in a separated file to be readable by both GMSH and GetDP. // - "Gamma" is a special word used by GMSH/GetDP, that is why the boundary is named "Gama", with one "m"... // Do not forget to let a blank line at the end, this could make GMSH crash...
Direct link to file `getdp/LaplacianDirichlet/GMSH_GETDP/param.geo'
LaplacianDirichlet.geo: creation of the geometry with GMSH
// File "LaplacianDirichlet.geo".
// This file is exactly the same as "LaplacianNeumann.geo" EXCEPT
// for the creation of the Physical Entity "Gama" (the boundary), at the end of the file
// We include the file containing the numbering of the geometry.
Include "param.geo";
//Caracteristic length of the finite elements (reffinement is also possible after the mesh is built):
lc = 0.05;
// The parameters of the border of the domain :
x_max = 1;
x_min = 0;
y_max= 1;
y_min = 0;
//Creation of the 4 angle points of the domain Omega (=square)
p1 = newp; Point(p1) = {x_min,y_min,0,lc};
p2 = newp; Point(p2) = {x_min,y_max,0,lc};
p3 = newp; Point(p3) = {x_max,y_max,0,lc};
p4 = newp; Point(p4) = {x_max,y_min,0,lc};
//The four edges of the square
L1 = newreg; Line(L1) = {p1,p2};
L2 = newreg; Line(L2) = {p2,p3};
L3 = newreg; Line(L3) = {p3,p4};
L4 = newreg; Line(L4) = {p4,p1};
// Line Loop (= boundary of the square)
Bound = newreg; Line Loop(Bound) = {L1,L2,L3,L4};
//Surface of the square
SurfaceOmega = newreg; Plane Surface(SurfaceOmega) = {Bound};
// To conclude, we define the physical entities, that is "what GetDP could see/use".
// Both "Omega" and "Gama" are imported from the file "param.geo".
Physical Surface(Omega) = {SurfaceOmega};
Physical Line(Gama) = {L1,L2,L3,L4}; // the Physical Line Gama is composed of the four lines of te boundary (not of the Line Loop !)
// Do not forget to let a blank line at the end, this could make GMSH crash...
Direct link to file `getdp/LaplacianDirichlet/GMSH_GETDP/LaplacianDirichlet.geo'
LaplacianDirichlet.pro: weak formulation
// File LaplacianDirichlet.pro
// This file is similar to LaplacianDirichlet.pro
// Only changes are detailed.
// we import the indices of Gama and Omega
Include "param.geo";
// Group
//======
// We have 2 Groups : Omega and Gama (boundary)
Group{
Omega = Region[{Omega}];
Gama = Region[{Gama}];
}
//Again note that "Gamma" is a syntaxic word of GetDP
// That is why we write here "Gama" and not "Gamma".
// (not a mistake from the author :-))
// Function
//=========
Function{
// Pi is a special value in GetDp (=3.1415...)
Coef = Pi;
// Definition of the function f(x,y)
f[] = -(1+2*Coef*Coef)*Sin[Coef*X[]]*Sin[Coef*Y[]];
// Here f exist on Omega AND Gama. As a consequence, we have to let "f" lives everywhere,
// and we let the bracket [] empty.
}
//Jacobian
//========
Jacobian {
{ Name JVol ;
Case {
{ Region All ; Jacobian Vol ; }
}
}
{ Name JSur ;
Case {
{ Region All ; Jacobian Sur ; }
}
}
{ Name JLin ;
Case {
{ Region All ; Jacobian Lin ; }
}
}
}
//Integration (parameters)
//=======================
Integration {
{ Name I1 ;
Case {
{ Type Gauss ;
Case {
{ GeoElement Point ; NumberOfPoints 1 ; }
{ GeoElement Line ; NumberOfPoints 4 ; }
{ GeoElement Triangle ; NumberOfPoints 6 ; }
{ GeoElement Quadrangle ; NumberOfPoints 7 ; }
{ GeoElement Tetrahedron ; NumberOfPoints 15 ; }
{ GeoElement Hexahedron ; NumberOfPoints 34 ; }
}
}
}
}
}
//Contraint
//=============
// This part is new, compare to LaplacianDirichlet.pro.
Constraint{
{Name DirichletBC; Type Assign;
Case{
{Region Gama; Value 0; }
}
}
}
/*
The Dirichlet Boundary Condition is here called "DirichletBC.
"Assign": type means that it is a Dirichlet type condition
"Region": domain where the condition is applied.
"Value": value assigned (here 0).
*/
//FunctionSpace
//=============
FunctionSpace{
{ Name Vh; Type Form0;
BasisFunction{
{Name wn; NameOfCoef vn; Function BF_Node;
Support Omega; Entity NodesOf[All];}
}
// Contrary to Neumann case, we had here the constraint :
Constraint{
{NameOfCoef vn; EntityType NodesOf;
NameOfConstraint DirichletBC;}
}
}
}
/* On the constraint:
- "NameOfCoef" : a constraint is applied to specific coefficients, here "vn" (in our example, there are the only coefficients
because of functions are P1)
- "Entitytype" : The constraint is applied on the nodes (e.g : not on the edge)
- "NameOfConstraint" : Last (but not least), we have to specify which Constraint is called.
With that definition, every function u (even the test-functions) of V_h satisfy the Dirichlet Boundary Condition:
u = 0 on Gama.
In other words, this spaces approximate the Sobolev space H^1_0(Omega).
*/
//(Weak) Formulation
//==================
Formulation{
{Name LaplacianDirichlet; Type FemEquation;
Quantity{
{Name u; Type Local; NameOfSpace Vh;}
}
Equation{
Galerkin{ [Dof{Grad u}, {Grad u}];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ Dof{u}, {u}];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ -f[], {u}];
In Omega; Jacobian JVol; Integration I1;}
}
}
}
/*
The variationnal formulation can be read as :
search "Dof{u}" in V_h such that, for every "{u}" in V_h,
\int_{\Omega} Grad( Dof{u}) . Grad( {u}) d\Omega + \int_{\Omega} Dof{u}.{u} d\Omega = 0
The Dirichlet Boundary Condition is contained in the function space V_h !
*/
// Resolution (of the problem)
//============================
Resolution{
// nothing change ... (except the name :-)
{Name LaplacianDirichlet;
System{
{Name Syst; NameOfFormulation LaplacianDirichlet;}
}
Operation{
Generate[Syst]; Solve[Syst]; SaveSolution[Syst];
}
}
}
//Post Processing
//===============
PostProcessing{
{Name LaplacianDirichlet; NameOfFormulation LaplacianDirichlet;
Quantity{
{Name u; Value {Local{[{u}];In Omega;Jacobian JVol;}}}
// We also ask the computation of the absolute value of "u" and the function "f".
//These new variable are called respectively "AbsU" and "f"
{Name AbsU; Value {Local{[Norm[{u}]];In Omega;Jacobian JVol;}}}
{Name f; Value {Local{[f[]];In Omega;Jacobian JVol;}}}
}
}
}
//Post Operation
//==============
PostOperation{
{Name Map_u; NameOfPostProcessing LaplacianDirichlet;
Operation{
Print[u, OnElementsOf Omega, File "u_Dirichlet.pos"];
// Plot of Abs(u) and f
Print[AbsU, OnElementsOf Omega, File "u_Abs_Dirichlet.pos"];
Print[f, OnElementsOf Omega, File "f.pos"];
}
}
}
Direct link to file `getdp/LaplacianDirichlet/GMSH_GETDP/LaplacianDirichlet.pro'