Tutorial/Laplace equation with Dirichlet boundary condition
Contents
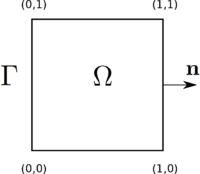
The considered problem
In this problem, we consider a Laplace equation, as in that example, except that the boundary condition is here of Dirichlet type. To model this in GetDP, we will introduce a "Constraint". We assume that the reader has already studied the previous example.
As in the example with a Neumann boundary condition, we considered the unit square $\Omega = [0,1]\times[0,1]$ and we seek the function $u$, solution of the following problem \begin{equation} \begin{cases}\label{eq:problemU} -\Delta u + u = f & \text{in } \Omega,\\ \displaystyle{u = 0} & \text{on }\Gamma, \end{cases} \end{equation} where $\Gamma = \partial\Omega$ is the boundary of $\Omega$ and $\displaystyle{\Delta = \frac{\partial^2}{\partial x_1^2} + \frac{\partial^2}{\partial x_2^2} }$ is the Laplace operator.
To simplify, we suppose that the function $f$ is defined by $$ \forall (x,y)\in [0,1]^2,\qquad f(x,y) = -(1+2\pi^2)\sin(\pi x)\sin(\pi y). $$ As a consequence, the unique solution $u$ of the problem \eqref{eq:problemU} is clearly given by $$ \forall (x,y)\in [0,1]^2, \qquad u(x,y) = -\sin(\pi x)\sin(\pi y). $$ To solve problem \eqref{eq:problemU} using the finite element method, we write its weak formulation: \begin{equation}\label{eq:WeakFormulation} \left\{\begin{array}{l} \text{Find } u\in H^1_0(\Omega) \text{ such that, }\\ \displaystyle{\forall v\in H^1_0(\Omega), \qquad \int_{\Omega} \nabla u\cdot\nabla v \;{\rm d}\Omega + \int_{\Omega}uv \;{\rm d}\Omega - \int_{\Omega} fv\;{\rm d}\Omega = 0}, \end{array}\right. \end{equation} where the functions $v$ are the test functions and $H^1_0(\Omega) = \left\{ v \in H^1(\Omega) \text{ such that } v|_{\Gamma} = 0\right\}$.
Outline of the program
The proposed solution is composed by 3 different files:
- param.geo
- Auxiliary file that contains the index number associated with the geometry.
- LaplacianDirichlet.geo
- GMSH file, used to build both the square $\Omega$ and its boundary $\Gamma$. Except for the building of $\Gamma$, this file is the same as in the previous example.
- LaplacianDirichlet.pro
- GetDP file, contains the weak formulation \eqref{eq:WeakFormulation} of the problem \eqref{eq:problemU}. The main difference between this example and the Neumann case is the addition of the (Dirichlet) Constraint, which is located in this GetDP file.
param.geo: the auxiliary file
// File "param.geo" //Numbers that caracterise the interior of the square (Omega) and its boundary (Gama): Omega = 1000; Gama = 1001; // Three remarks on these numbers : // - They are arbitrary choosen. // - They are placed in a separated file to be readable by both GMSH and GetDP. // - "Gamma" is a special word used by GMSH/GetDP, that is why the boundary is named "Gama", with one "m"... // Do not forget to let a blank line at the end, this could make GMSH crash...
Direct link to file `LaplacianDirichlet/GMSH_GETDP/param.geo'
LaplacianDirichlet.geo: creation of the geometry with GMSH
// File "LaplacianDirichlet.geo".
// This file is exactly the same as "LaplacianNeumann.geo" EXCEPT
// for the creation of the Physical Entity "Gama" (the boundary), at the end of the file
// We include the file containing the numbering of the geometry.
Include "param.geo";
//Caracteristic length of the finite elements (reffinement is also possible after the mesh is built):
lc = 0.05;
// The parameters of the border of the domain :
x_max = 1;
x_min = 0;
y_max= 1;
y_min = 0;
//Creation of the 4 angle points of the domain Omega (=square)
p1 = newp; Point(p1) = {x_min,y_min,0,lc};
p2 = newp; Point(p2) = {x_min,y_max,0,lc};
p3 = newp; Point(p3) = {x_max,y_max,0,lc};
p4 = newp; Point(p4) = {x_max,y_min,0,lc};
//The four edges of the square
L1 = newreg; Line(L1) = {p1,p2};
L2 = newreg; Line(L2) = {p2,p3};
L3 = newreg; Line(L3) = {p3,p4};
L4 = newreg; Line(L4) = {p4,p1};
// Line Loop (= boundary of the square)
Bound = newreg; Line Loop(Bound) = {L1,L2,L3,L4};
//Surface of the square
SurfaceOmega = newreg; Plane Surface(SurfaceOmega) = {Bound};
// To conclude, we define the physical entities, that is "what GetDP could see/use".
// Both "Omega" and "Gama" are imported from the file "param.geo".
Physical Surface(Omega) = {SurfaceOmega};
Physical Line(Gama) = {L1,L2,L3,L4}; // the Physical Line Gama is composed of the four lines of te boundary (not of the Line Loop !)
// Do not forget to let a blank line at the end, this could make GMSH crash...
Direct link to file `LaplacianDirichlet/GMSH_GETDP/LaplacianDirichlet.geo'
LaplacianDirichlet.pro: weak formulation
// File LaplacianDirichlet.pro
// This file is similar to LaplacianDirichlet.pro
// Only changes are detailed.
// we import the indices of Gama and Omega
Include "param.geo";
// Group
//======
// We have 2 Groups : Omega and Gama (boundary)
Group{
Omega = Region[{Omega}];
Gama = Region[{Gama}];
}
//Again note that "Gamma" is a syntaxic word of GetDP
// That is why we write here "Gama" and not "Gamma".
// (not a mistake from the author :-))
// Function
//=========
Function{
// Pi is a special value in GetDp (=3.1415...)
Coef = Pi;
// Definition of the function f(x,y)
f[] = -(1+2*Coef*Coef)*Sin[Coef*X[]]*Sin[Coef*Y[]];
// Here f exist on Omega AND Gama. As a consequence, we have to let "f" lives everywhere,
// and we let the bracket [] empty.
}
//Jacobian
//========
Jacobian {
{ Name JVol ;
Case {
{ Region All ; Jacobian Vol ; }
}
}
{ Name JSur ;
Case {
{ Region All ; Jacobian Sur ; }
}
}
{ Name JLin ;
Case {
{ Region All ; Jacobian Lin ; }
}
}
}
//Integration (parameters)
//=======================
Integration {
{ Name I1 ;
Case {
{ Type Gauss ;
Case {
{ GeoElement Point ; NumberOfPoints 1 ; }
{ GeoElement Line ; NumberOfPoints 4 ; }
{ GeoElement Triangle ; NumberOfPoints 6 ; }
{ GeoElement Quadrangle ; NumberOfPoints 7 ; }
{ GeoElement Tetrahedron ; NumberOfPoints 15 ; }
{ GeoElement Hexahedron ; NumberOfPoints 34 ; }
}
}
}
}
}
//Contraint
//=============
// This part is new, compare to LaplacianDirichlet.pro.
Constraint{
{Name DirichletBC; Type Assign;
Case{
{Region Gama; Value 0; }
}
}
}
/*
The Dirichlet Boundary Condition is here called "DirichletBC.
"Assign": type means that it is a Dirichlet type condition
"Region": domain where the condition is applied.
"Value": value assigned (here 0).
*/
//FunctionSpace
//=============
FunctionSpace{
{ Name Vh; Type Form0;
BasisFunction{
{Name wn; NameOfCoef vn; Function BF_Node;
Support Omega; Entity NodesOf[All];}
}
// Contrary to Neumann case, we had here the constraint :
Constraint{
{NameOfCoef vn; EntityType NodesOf;
NameOfConstraint DirichletBC;}
}
}
}
/* On the constraint:
- "NameOfCoef" : a constraint is applied to specific coefficients, here "vn" (in our example, there are the only coefficients
because of functions are P1)
- "Entitytype" : The constraint is applied on the nodes (e.g : not on the edge)
- "NameOfConstraint" : Last (but not least), we have to specify which Constraint is called.
With that definition, every function u (even the test-functions) of V_h satisfy the Dirichlet Boundary Condition:
u = 0 on Gama.
In other words, this spaces approximate the Sobolev space H^1_0(Omega).
*/
//(Weak) Formulation
//==================
Formulation{
{Name LaplacianDirichlet; Type FemEquation;
Quantity{
{Name u; Type Local; NameOfSpace Vh;}
}
Equation{
Galerkin{ [Dof{Grad u}, {Grad u}];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ Dof{u}, {u}];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ -f[], {u}];
In Omega; Jacobian JVol; Integration I1;}
}
}
}
/*
The variationnal formulation can be read as :
search "Dof{u}" in V_h such that, for every "{u}" in V_h,
\int_{\Omega} Grad( Dof{u}) . Grad( {u}) d\Omega + \int_{\Omega} Dof{u}.{u} d\Omega = 0
The Dirichlet Boundary Condition is contained in the function space V_h !
*/
// Resolution (of the problem)
//============================
Resolution{
// nothing change ... (except the name :-)
{Name LaplacianDirichlet;
System{
{Name Syst; NameOfFormulation LaplacianDirichlet;}
}
Operation{
Generate[Syst]; Solve[Syst]; SaveSolution[Syst];
}
}
}
//Post Processing
//===============
PostProcessing{
{Name LaplacianDirichlet; NameOfFormulation LaplacianDirichlet;
Quantity{
{Name u; Value {Local{[{u}];In Omega;Jacobian JVol;}}}
// We also ask the computation of the absolute value of "u" and the function "f".
//These new variable are called respectively "AbsU" and "f"
{Name AbsU; Value {Local{[Norm[{u}]];In Omega;Jacobian JVol;}}}
{Name f; Value {Local{[f[]];In Omega;Jacobian JVol;}}}
}
}
}
//Post Operation
//==============
PostOperation{
{Name Map_u; NameOfPostProcessing LaplacianDirichlet;
Operation{
Print[u, OnElementsOf Omega, File "u_Dirichlet.pos"];
// Plot of Abs(u) and f
Print[AbsU, OnElementsOf Omega, File "u_Abs_Dirichlet.pos"];
Print[f, OnElementsOf Omega, File "f.pos"];
}
}
}
Direct link to file `LaplacianDirichlet/GMSH_GETDP/LaplacianDirichlet.pro'
How to launch
The procedure is the same as described in this example, but we recall it here. Let us recall that all files (.geo and .pro) must be located in the same directory. We just describe the procedure using a terminal.
- Meshing the domain
In the right directory, type:
- gmsh -LaplacianDirichlet.geo -algo iso -2
(again, the algorithm could be another one) After that, a file LaplacianDirichlet.msh should have been created.
- Solving the problem
Type the following command in the terminal:
- getdp LaplacianDirichlet.pro -solve -pos
And answer "1" to the two questions.
- Displaying the result
Simply open the .pos files with GMSH.
Result
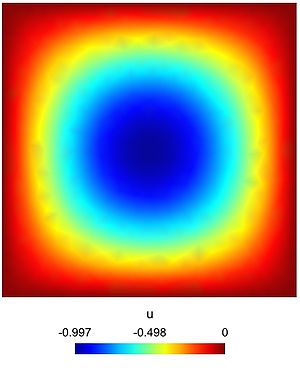
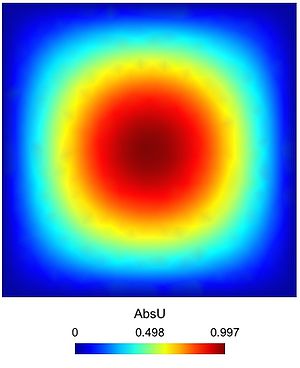
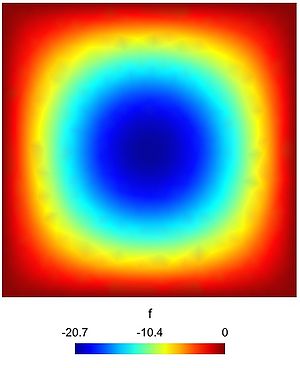
Here is the result obtained with GMSH/GetDP. The first and second pictures show respectively the solution $u$ and its absolute value. The third figure represents the function $f$.
All files
A zipfile containing all files (.geo, .pro, .mesh and .pos) can be downloaded here.