Difference between revisions of "Tutorial/Eigenvalue problems"
(Created page with "{{metamodel|academic_eigenvalues}} {{mytexdefs}} == Introduction == This academic example introduces the numerical solution of eigenvalue problems. The Helmholtz equation (...") |
m (Geuzaine moved page Academic example: Eigenvalue problems to Tutorial/Eigenvalue problems) |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 11: | Line 11: | ||
provide the first eigenvalues and the associated eigenfunctions (i.e. the first possible solutions). | provide the first eigenvalues and the associated eigenfunctions (i.e. the first possible solutions). | ||
| − | $\rightarrow$ To run the | + | $\rightarrow$ To run the model, open '''main.pro''' with Gmsh. |
| − | == Description of the | + | == Description of the model == |
==== Differential formulations ==== | ==== Differential formulations ==== | ||
| Line 31: | Line 31: | ||
\begin{cases} | \begin{cases} | ||
\Delta \mathbf{u} + k^2 \mathbf{u} = 0 & \text{ in } \Omega, \\ | \Delta \mathbf{u} + k^2 \mathbf{u} = 0 & \text{ in } \Omega, \\ | ||
| − | \mathbf{n}\ | + | \mathbf{n}\times\mathbf{u} = 0 & \text{ on } \partial\Omega, |
\end{cases} | \end{cases} | ||
\end{equation} | \end{equation} | ||
| Line 68: | Line 68: | ||
: where $H_0(\Omega,\Curl) = \{\mathbf{v} \in \mathbf{L}_2(\Omega) \text{ such that } \Curl{\mathbf{v}} \in \mathbf{L}_2(\Omega) \text{ and } \mathbf{n}\cdot\mathbf{v}|_{\partial\Omega} = 0\}$. | : where $H_0(\Omega,\Curl) = \{\mathbf{v} \in \mathbf{L}_2(\Omega) \text{ such that } \Curl{\mathbf{v}} \in \mathbf{L}_2(\Omega) \text{ and } \mathbf{n}\cdot\mathbf{v}|_{\partial\Omega} = 0\}$. | ||
| − | These formulations are coded in <code>formulation.pro</code>. The functional spaces are based on nodal elements for the scalar-wave problem (<code>Form0</code>) and edge elements for the vector-wave problem (<code> | + | These formulations are coded in <code>formulation.pro</code>. The functional spaces are based on nodal elements for the scalar-wave problem (<code>Form0</code>) and edge elements for the vector-wave problem (<code>Form1P</code> in 1D and 2D, and <code>Form1</code> in 3D). The homogeneous Dirichlet boundary condition are prescribed through constraints in the functional spaces. |
==== Eigenvalue algebraic problem ==== | ==== Eigenvalue algebraic problem ==== | ||
Latest revision as of 21:12, 19 April 2015
|
ERROR in secure-include.php: /onelab_files/academic_eigenvalues/README.txt does not look like a URL, and doesn't exist as a file. |
 
|
|---|
|
Download model archive (academic_eigenvalues.zip) |
\(\renewcommand{\vec}[1]{\mathbf{#1}} \newcommand{\Grad}[1]{\mathbf{\text{grad}}\,{#1}} \newcommand{\Curl}[1]{\mathbf{\text{curl}}\,{#1}} \newcommand{\Div}[1]{\text{div}\,{#1}} \newcommand{\Real}[1]{\text{Re}({#1})} \newcommand{\Imag}[1]{\text{Im}({#1})} \newcommand{\pvec}[2]{{#1}\times{#2}} \newcommand{\psca}[2]{{#1}\cdot{#2}} \newcommand{\E}[1]{\,10^{#1}} \newcommand{\Ethree}{{\mathbb{E}^3}} \newcommand{\Etwo}{{\mathbb{E}^2}} \newcommand{\Units}[1]{[\mathrm{#1}]} \)
Contents
Introduction
This academic example introduces the numerical solution of eigenvalue problems. The Helmholtz equation (scalar and vector versions) is considered with homogeneous Dirichlet boundary conditions, for different basic geometries (i.e. linear, squared, circular and cuboid domain). These problems have a family of solutions. The eigenvalue solver used for this example provide the first eigenvalues and the associated eigenfunctions (i.e. the first possible solutions).
$\rightarrow$ To run the model, open main.pro with Gmsh.
Description of the model
Differential formulations
We consider differential problems based on the scalar and vector Helmholtz equations with homogeneous Dirichlet boundary conditions. Let the bounded domain $\Omega\subset\mathbb{R}^d$, whose boundary is denoted $\partial\Omega$.
- For the scalar-wave eigenvalue problem, we are looking for a scalar value $k$ and a scalar field $u(\mathbf{x})$ that are the solution of
\begin{equation} \begin{cases} \Delta u + k^2 u = 0 & \text{ in } \Omega,\\ u = 0 & \text{ on } \partial\Omega, \end{cases} \end{equation}
- where $\Delta$ is the Laplace operator.
- For the vector-wave eigenvalue problem, we are looking for a scalar value $k$ and a vector field $\mathbf{u}(\mathbf{x})$ that are the solution of
\begin{equation} \begin{cases} \Delta \mathbf{u} + k^2 \mathbf{u} = 0 & \text{ in } \Omega, \\ \mathbf{n}\times\mathbf{u} = 0 & \text{ on } \partial\Omega, \end{cases} \end{equation}
- where $\Delta$ is the vector version of the Laplace operator and $\mathbf{n}(\mathbf{x})$ is the outward unit normal to $\partial\Omega$.
The solution of these problems is not unique [1]. There is a family of eigenvalues $k_i$ associated to eigenfunctions $u_i(\mathbf{x})$ or $\mathbf{u}_i(\mathbf{x})$ that solve these problems.
Finite element schemes
The eigenvalue problems are solved by using finite element schemes based on the following weak forms.
- For the scalar-wave problem, the weak form is
\begin{equation} \left\{ \begin{array}{l} \displaystyle{\text{Find } u \in H_0(\Omega,\Grad) \text{ such that}}\\ \displaystyle{\forall u'\in H_0(\Omega,\Grad),\qquad \int_{\Omega}\Grad u\cdot\Grad u'\;{\rm d}\Omega - \int_{\Omega}k^2 uu'\;{\rm d}\Omega =0,} \end{array}\right. \end{equation}
- where $H_0(\Omega,\Grad) = \{v \in L_2(\Omega) \text{ such that } \Grad v \in \mathbf{L}_2(\Omega) \text{ and } v|_{\partial\Omega} = 0\}$.
- For the vector-wave problem, the weak form is (see e.g. [2], chapter 7)
\begin{equation} \left\{ \begin{array}{l} \displaystyle{\text{Find } \mathbf{u} \in H_0(\Omega,\Curl) \text{ such that}}\\ \displaystyle{\forall \mathbf{u}'\in H_0(\Omega,\Curl),\qquad \int_{\Omega} \Curl{\mathbf{u}}\cdot\Curl{\mathbf{u}'}\;{\rm d}\Omega - \int_{\Omega}k^2 \mathbf{u}\cdot\mathbf{u}'\;{\rm d}\Omega =0,} \end{array}\right. \end{equation}
- where $H_0(\Omega,\Curl) = \{\mathbf{v} \in \mathbf{L}_2(\Omega) \text{ such that } \Curl{\mathbf{v}} \in \mathbf{L}_2(\Omega) \text{ and } \mathbf{n}\cdot\mathbf{v}|_{\partial\Omega} = 0\}$.
These formulations are coded in formulation.pro. The functional spaces are based on nodal elements for the scalar-wave problem (Form0) and edge elements for the vector-wave problem (Form1P in 1D and 2D, and Form1 in 3D). The homogeneous Dirichlet boundary condition are prescribed through constraints in the functional spaces.
Eigenvalue algebraic problem
The final discrete problem reads $$ [\vec{A}-k^2 \vec{I}] \vec{x} = \vec{0}, $$ where $\vec{x}$ contains all discrete unknowns of the problem. In GetDP, the eigenvalues and eigenvectors of this algebraic system are provided by numerical algorithms of SLEPc or ARPACK libraries.
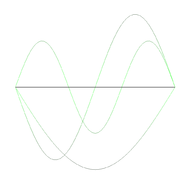
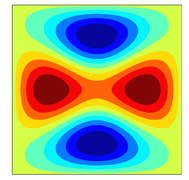
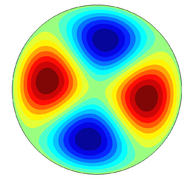
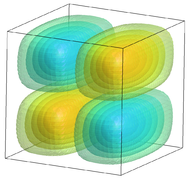
Some results
Here are some snapshots of eigenfunctions for the scalar-wave eigenvalue problem with different domains.
References
- ↑ L.C. Evans, Partial Differential Equations. Second edition. American Mathematical Society, 2010
- ↑ J. Jin, The Finite Element Method in Electromagnetics. Second edition. John Wiley & Sons, 2002
|
ERROR in secure-include.php: /onelab_files/academic_eigenvalues/COPYING.txt does not look like a URL, and doesn't exist as a file. |