Tutorial/Wave equation with Dirichlet boundary control
Contents
The considered problem
In this problem, we consider a Wave equation with a Dirichlet control on a part of the boundary, and homogeneous Dirichlet or Neumann condition on the other part. To model this in GetDP, we will introduce a "Constraint" with "TimeFunction". We assume that the reader has already studied the parabolic example on the Heat equation.
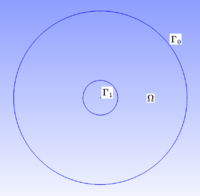
We considered the annulus $\Omega = \mathcal D (0, 1) \setminus \mathcal D (0, 0.2)$ and we seek the functions $w_N$ and $w_D$, respective solutions of the following problems
\begin{equation} \begin{cases}\label{eq:problemNeu} \dfrac{\partial^2}{\partial t^2} w_N(x,t) -\Delta w_N(x,t) = 0 & \forall x \in \Omega, t\geq0\\ \dfrac{\partial w_N}{\partial \mathbf{n}}(x,t) = 0 & \forall x \in \Gamma_0, t \geq0\\ w_N(x,t) = u(x,t) & \forall x \in \Gamma_1, t \geq0. \end{cases} \end{equation}
\begin{equation} \begin{cases}\label{eq:problemDir} \dfrac{\partial^2}{\partial t^2} w_D(x,t) -\Delta w_D(x,t) = 0 & \forall x \in \Omega, t\geq0\\ w_D(x,t) = 0 & \forall x \in \Gamma_0, t \geq0\\ w_D(x,t) = u(x,t) & \forall x \in \Gamma_1, t \geq0. \end{cases} \end{equation}
where $\Gamma_0 = \partial \mathcal D (0, 1)$ is the boundary of $\mathcal D (0, 1)$, $\Gamma_1 = \partial \mathcal D (0, 0.2)$ is the boundary of $\mathcal D (0, 0.2)$ and $\displaystyle{\Delta = \frac{\partial^2}{\partial x_1^2} + \frac{\partial^2}{\partial x_2^2} }$ is the Laplace operator.
To simplify, we suppose that the control $u$ is defined by $$ \forall (x,y)\in \Gamma_1, t\geq0 \qquad u(x,y,t) = u(t) = 5\sin(2\pi t). $$
Physically, these problems model the vibration of a membrane on the annulus over time. The Dirichlet boundary condition models the fact that the membrane is fixed on the boundary $\Gamma_0$ at $0$, as the Neumann boundary condition models the fact that the membrane is let free on the boundary $\Gamma_0$ to move up and down. Furthermore, the control $u$ corresponds to an up and down motion of the boundary $\Gamma_1$ of the membrane oscillating between -5 and 5.
To solve problems \eqref{eq:problemNeu} and \eqref{eq:problemDir} using the finite element method, we write their weak formulations:
\begin{equation}\label{eq:WeakFormulationNeu} \left\{\begin{array}{l} \text{Find } v_N\in C^2([0,\infty),\mathcal H_N) \text{ such that, }\\ \displaystyle{\forall \varphi\in \mathcal H_N, t\geq0, \qquad \int_{\Omega}\dfrac{d^2 v_N}{dt^2} \varphi \;{\rm d}\Omega + \int_{\Omega} \nabla v_N\cdot\nabla \varphi \;{\rm d}\Omega = 0}, \end{array}\right. \end{equation}
\begin{equation}\label{eq:WeakFormulationDir} \left\{\begin{array}{l} \text{Find } v_D\in C^2([0,\infty),\mathcal H_D) \text{ such that, }\\ \displaystyle{\forall \varphi\in \mathcal H_D, t\geq0, \qquad \int_{\Omega}\dfrac{d^2 v_D}{dt^2} \varphi \;{\rm d}\Omega + \int_{\Omega} \nabla v_D\cdot\nabla \varphi \;{\rm d}\Omega = 0}, \end{array}\right. \end{equation} where $\mathcal H_N = \{w \in H^1(\Omega) \mid w = u \text{ on } \Gamma_1 \}$, $\mathcal H_D = \{w \in H^1(\Omega) \mid w = 0 \text{ on } \Gamma_0, \; w = u \text{ on } \Gamma_1 \}$ and the functions $\varphi$ are the test functions.
To solve these equations, we use the DtDtDof keyword of GetDP in the Formulation group to specify the second derivative in time in the weak formulation, as in the Resolution group, we use the TimeLoopNewmark keyword to indicate that we need a second order finite difference time scheme.
There is an additional difficulty in this case than in the Heat equation. Indeed, here we are dealing with a second-order PDE, which implies that the time scheme needs two steps to be correctly initialized. In other words, we have to initialized both position and velocity of the membrane.
We have to take that into account in the Resolution group in GetDP. If the initial velocity is equal to zero, then we just have to double the initialization InitSolution, this will put the initial state in the two first steps of the time discretisation. However, if we want to solve a system with non-zero initial velocity, we have to use a trick. The idea is to initialize the velocity using a weak formulation, which has to be zero when the Time Step is greater than 2. We invite the reader to read carefully the Formulation group of the Wave.pro file to clarify what we mean here. Then, we solve separetely the second time step and the following, as one can read in the Resolution group of the Wave.pro file.
Outline of the program
The proposed solution is composed by 2 different files:
- Annulus.geo
- GMSH file, used to build both the square $\Omega$ and its boundary $\Gamma_0$ and $\Gamma_1$.
- Wave.pro
- GetDP file, contains the weak formulations \eqref{eq:WeakFormulationNeu} and \eqref{eq:WeakFormulationDir} of the problems \eqref{eq:problemNeu} and \eqref{eq:problemDir}.
Annulus.geo: creation of the geometry with GMSH
/* -----------------------
File Annulus.geo
----------------------- */
// Mesh step h :
h = 0.025;
/*==============*/
/* Large Circle */
/*==============*/
// Points :
Point(1) = {0,0,0,h};
Point(2) = {1,0,0,h};
Point(3) = {0,1,0,h};
Point(5) = {-1,0,0,h};
Point(6) = {0,-1,0,h};
// Arcs :
Circle(1) = {2,1,3};
Circle(2) = {3,1,5};
Circle(3) = {5,1,6};
Circle(4) = {6,1,2};
// Circle :
Line Loop(1) = {1,2,3,4};
/*===============*/
/* Little Circle */
/*===============*/
// Points :
Point(200) = {0.2,0,0,h};
Point(300) = {0,0.2,0,h};
Point(500) = {-0.2,0,0,h};
Point(600) = {0,-0.2,0,h};
// Arcs :
Circle(100) = {200,1,300};
Circle(200) = {300,1,500};
Circle(300) = {500,1,600};
Circle(400) = {600,1,200};
// Circle :
Line Loop(100) = {100,200,300,400};
/*=======*/
/* Omega */
/*=======*/
// Annulus : The surface between the little circle and the large circle
Plane Surface(1) = {1, 100};
/*===================*/
/* Physical Entities */
/*===================*/
// Gama0
Physical Line(1001) = {1,2,3,4};
// Gama1
Physical Line(1002) = {100,200,300,400};
// Omega
Physical Surface(1005) = {1};
Direct link to file `Wave/GMSH_GETDP/Annulus.geo'
Wave.pro: weak formulations
/* -----------------------
File Wave.pro
----------------------- */
/*======================
Geometrical Entities
======================*/
Group {
// Boundary
Gama0 = Region[ 1001 ];
Gama1 = Region[ 1002 ];
// The Domain
Omega = Region[ 1005 ];
// The Boundary And The Domain
AllOmega = Region[{Omega,Gama0,Gama1}];
}
/*=====================
Some Functions
=====================*/
Function {
// Initial Position of the membrane
InitialState[AllOmega] = 10*Exp[-25*((X[]+0.5)*(X[]+0.5)+(Y[]+0.5)*(Y[]+0.5))] - 5*Exp[-50*((X[]+0.3)*(X[]+0.3)+(Y[]+0.5)*(Y[]+0.5))] - 10*Exp[-45*((X[]-0.5)*(X[]-0.5)+(Y[]-0.5)*(Y[]-0.5))];
// Initial Velocity of the membrane
InitialVelocity[AllOmega] = -Exp[-25*((X[]+0.5)*(X[]+0.5)+(Y[]-0.6)*(Y[]-0.6))];
// Control (Up and down oscillations)
u[] = 5*Sin[2*Pi*$Time];
// Time Discretization
t0 = 0.;
T = 2.;
dt = 0.01;
// Type of Scheme (See Newmark on the manual)
beta = 0.25;
gamma = 0.5;
}
/*===============================
Constraints and Initial State
===============================*/
Constraint {
// Initial State
{ Name InitialData; Type Init;
Case {
{ Region Omega; Value InitialState[]; }
}
}
// Boundary control
{ Name Displacement; Type Assign;
Case {
{ Region Gama1; Value 1.; TimeFunction u[]; }
}
}
// Boundary Dirichlet Condition (membrane fixed on Gama0)
{ Name Fixed; Type Assign;
Case {
{ Region Gama0; Value 0.; }
}
}
}
/*====================
Functional Spaces
====================*/
FunctionSpace {
{ Name VhNeu; Type Form0;
BasisFunction{
{ Name wn; NameOfCoef vn; Function BF_Node;
Support AllOmega; Entity NodesOf[All];}
}
Constraint {
{ NameOfCoef vn; EntityType NodesOf;
NameOfConstraint Displacement; }
{ NameOfCoef vn; EntityType NodesOf;
NameOfConstraint InitialData; }
}
}
{ Name VhDir; Type Form0;
BasisFunction{
{ Name wn; NameOfCoef vn; Function BF_Node;
Support AllOmega; Entity NodesOf[All];}
}
Constraint {
{ NameOfCoef vn; EntityType NodesOf;
NameOfConstraint Displacement; }
{ NameOfCoef vn; EntityType NodesOf;
NameOfConstraint Fixed; }
{ NameOfCoef vn; EntityType NodesOf;
NameOfConstraint InitialData; }
}
}
}
/*====================
Jacobian
====================*/
Jacobian {
{ Name JVol ;
Case {
{ Region All ; Jacobian Vol ; }
}
}
{ Name JSur ;
Case {
{ Region All ; Jacobian Sur ; }
}
}
{ Name JLin ;
Case {
{ Region All ; Jacobian Lin ; }
}
}
}
/*======================
Integral Parameters
======================*/
Integration {
{ Name I1 ;
Case {
{ Type Gauss ;
Case {
{ GeoElement Point ; NumberOfPoints 1 ; }
{ GeoElement Line ; NumberOfPoints 4 ; }
{ GeoElement Triangle ; NumberOfPoints 6 ; }
{ GeoElement Quadrangle ; NumberOfPoints 7 ; }
{ GeoElement Tetrahedron ; NumberOfPoints 15 ; }
{ GeoElement Hexahedron ; NumberOfPoints 34 ; }
}
}
}
}
}
/*======================
Weak formulations
======================*/
Formulation {
{ Name Wave; Type FemEquation;
Quantity{
{ Name w; Type Local; NameOfSpace VhNeu;}
{ Name v; Type Local; NameOfSpace VhDir;}
}
Equation{
// Membrane letting free, i.e. Neumann boundary condition on Gama0
// Taking the initial velocity into acount
Galerkin{ DtDof [ ($TimeStep < 2 ? 1 : 0) * Dof{w}, {w} ];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ -($TimeStep < 2 ? 1 : 0) * InitialVelocity[], {w} ];
In Omega; Jacobian JVol; Integration I1;}
// Weak formulation after the initialisation of the two first steps
Galerkin{ DtDtDof [ ($TimeStep < 2 ? 0 : 1) * Dof{w}, {w} ];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ ($TimeStep < 2 ? 0 : 1) * Dof{Grad w}, {Grad w} ];
In Omega; Jacobian JVol; Integration I1;}
// Membrane fixed, i.e. Dirichlet boundary condition on Gama0
// Taking the initial velocity into acount
Galerkin{ DtDof [ ($TimeStep < 2 ? 1 : 0) * Dof{v}, {v} ];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ -($TimeStep < 2 ? 1 : 0) * InitialVelocity[], {v} ];
In Omega; Jacobian JVol; Integration I1;}
// Weak formulation after the initialisation of the two first steps
Galerkin{ DtDtDof [ ($TimeStep < 2 ? 0 : 1) * Dof{v}, {v} ];
In Omega; Jacobian JVol; Integration I1;}
Galerkin{ [ ($TimeStep < 2 ? 0 : 1) * Dof{Grad v}, {Grad v} ];
In Omega; Jacobian JVol; Integration I1;}
}
}
}
/*======================
Resolution
======================*/
Resolution {
{ Name WaveSolver;
System{
{ Name SysWave; NameOfFormulation Wave;}
}
Operation{
// Initialisation
InitSolution[SysWave];
// Initialisation of the velocity
TimeLoopTheta[t0, t0 + dt, dt, 0.5 ] {
Generate[SysWave]; Solve[SysWave];
}
// Computation on [t0 + dt,T]
TimeLoopNewmark[ t0 + dt, T, dt, beta, gamma ] {
Generate[SysWave]; Solve[SysWave];
}
}
}
}
/*==============
Post Processing
==============*/
PostProcessing {
{ Name WaveSolver; NameOfFormulation Wave; NameOfSystem SysWave;
Quantity{
{ Name Free; Value {Local{[{w}]; In AllOmega; Jacobian JVol;}}}
{ Name Fixed; Value {Local{[{v}]; In AllOmega; Jacobian JVol;}}}
}
}
}
/*=============
Post Operation
=============*/
PostOperation {
{Name Map_Omega; NameOfPostProcessing WaveSolver;
Operation{
Print[Free, OnElementsOf AllOmega, File "WaveFreeOnOmega.pos"];
Print[Fixed, OnElementsOf AllOmega, File "WaveFixedOnOmega.pos"];
}
}
}
Direct link to file `Wave/GMSH_GETDP/Wave.pro'
How to launch
The procedure is the same as described in this example, but we recall it here. Let us recall that all files (.geo and .pro) must be located in the same directory. We just describe the procedure using a terminal.
- Meshing the domain
In the right directory, type:
- gmsh Annulus.geo -algo iso -2
After that, a file Annulus.msh should have been created.
- Solving the problem
Type the following command in the terminal:
- getdp Wave.pro -solve '#1' -pos '#1' -mesh Annulus.msh
- Displaying the result
Simply open the two .pos files with GMSH, and compare them to see the influence of the control on $\Gamma_1$ and the Neumann and Boundary conditions on $\Gamma_0$.
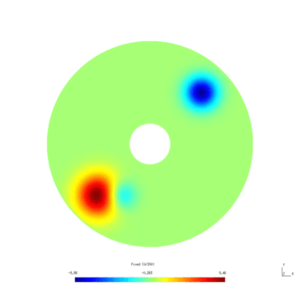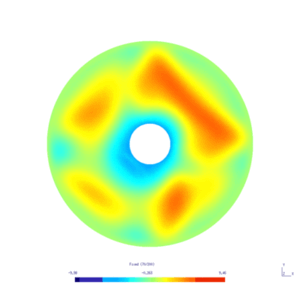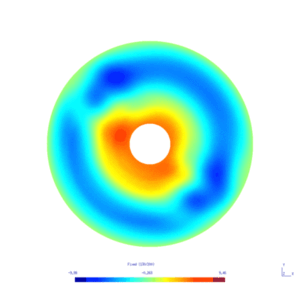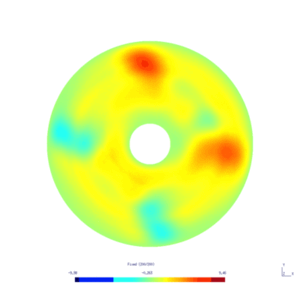
Results
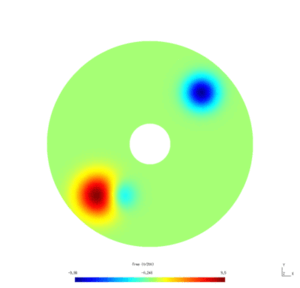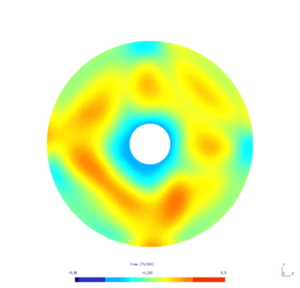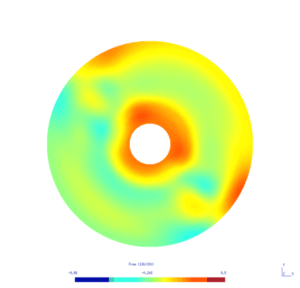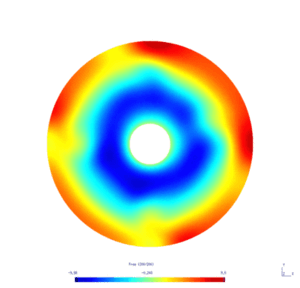
Here is the result obtained with GMSH/GetDP. The first and second pictures show respectively the solution $w_N$ and $w_D$, every ten steps.
All files
A zipfile containing all files (.geo, .pro, .mesh and .gif with all Time Steps, the .pos are too big) can be downloaded here.